Oscillator

An oscillator is a positive feedback electronic circuit in which the input signal and the feedback signal are in phase with each other. It can be used to generate oscillating signals such as square waves, triangular waves, sine waves, etc., without any external input.

Feedback in Electronic Circuits:

The process of injecting some portion of the output signal of a circuit back as input to the same circuit is known as feedback.

Consider the following system, which shows the amplification of input voltage $V_i$ by a factor "A".

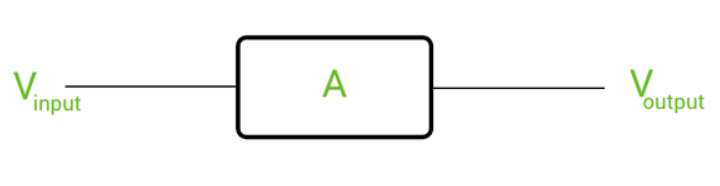
Output Voltage = Amplification Factor $\times$ Net Input Voltage

$V_o = A \times V_i \quad \text{(i)}$

Connecting feedback to the above system gives:

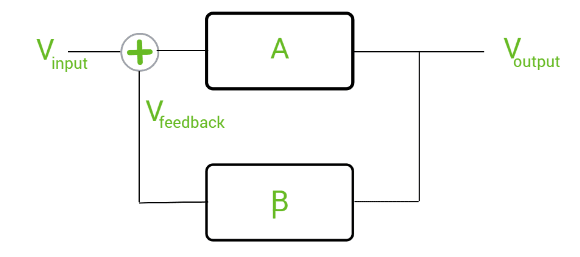
Here, $\beta$ is the fraction of the output voltage $V_o$ fed back as input to the system, i.e.,

$V_f = \beta V_o \quad \text{(ii)}$

Also, in the case of oscillators, the feedback element provides $0^\circ$ or $360^\circ$ of total phase shift to the feedback signal.

So, the total input to the system becomes $(V_i + V_f)$.

From equation (i), we get:

$V_o = A \times (V_i + V_f)$

$V_o = A V_i + A V_f$

$V_o = A V_i + A \beta V_o \quad \text{(from eq. (ii))}$

$V_o(1 - A\beta) = A V_i$

$\frac{V_o}{V_i} = \frac{A}{(1 – A\beta)}$

The gain of a system with positive feedback is given by $\frac{A}{(1 – A\beta)}$.

It can be clearly noted that whether the input signal in the system will be amplified, attenuated, or remain sustained depends on the value of $A\beta$.

Therefore, three cases arise:

Note that "A" represents the amplification of the signal without feedback, and "$\beta$" represents the fraction of the output voltage that is fed back to the system.

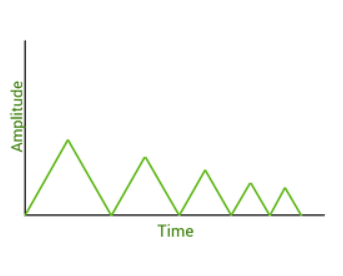
(Case 1) $A\beta < 1$:

Here, decaying oscillations are generated by the oscillator. Below is an example of decaying oscillations.

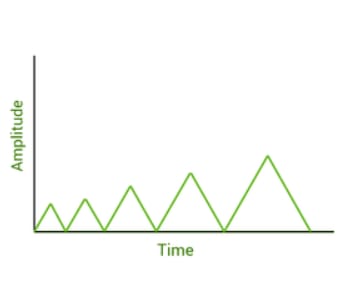
(Case 2) $A\beta > 1$:

Here, growing oscillations are generated. Below is an example of growing oscillations.

(Case 3) $A\beta = 1$:

Here, sustained oscillations are generated by the oscillator. Below is an example of sustained oscillations.

Therefore, sustained oscillations are generated only when $A\beta = 1$.

Criteria For Oscillations

• For an oscillator, there is no input ($V_s = 0$), so the feedback voltage $V_f$ must be sufficient to maintain the oscillations.

• To ensure this, the oscillator must satisfy a criterion called the Barkhausen criterion.

• Consider an inverting amplifier producing a $180^\circ$ phase shift between the input and output.

• To ensure positive feedback, there must be an additional $180^\circ$ phase shift between the output $V_o$ and the feedback voltage $V_f$. This ensures that the feedback voltage is in phase with the input, thereby ensuring positive feedback.

  

• $V_o = A V_i$ while $V_f = - \beta V_o$, where the negative sign indicates a $180^\circ$ phase shift between $V_o$ and $V_f$.

  $V_f = -A \beta V_i$

• For the oscillator, $V_i = 0$ and $V_f$ must drive the circuit; hence $V_f = V_i$.

  $\therefore V_i = -A\beta V_i$

  i.e., $-A\beta = 1 \quad \text{(i)}$

• The condition $-A \beta = 1$ is called the Barkhausen condition.

• From equation (i) we can write $A\beta = -1 + j0$, and by equating magnitudes,

  $| A \beta | = 1 \quad \text{(ii)}$

• To ensure the phase of $V_f$ is the same as the phase of $V_i$, i.e., to ensure positive feedback, the total phase shift around the loop must be $180^\circ$ by the forward path plus $180^\circ$ by the feedback path, which totals $360^\circ$.

• The two conditions discussed above, which are required for the circuit to function as an oscillator, are called the Barkhausen criterion for oscillation.

The Barkhausen criterion states that:

1. The total phase shift around a loop, as the signal proceeds from the input through the amplifier and feedback network back to the input again, completing a loop, is precisely $0^\circ$ or $360^\circ$, or an integral multiple of $2\pi$ radians.

2. The magnitude of the product of the open-loop gain of the amplifier (A) and the feedback factor $\beta$ is unity, i.e., $| A \beta | = 1$.

When these conditions are satisfied, the circuit functions as an oscillator, producing sustained oscillations with constant frequency and amplitude. In reality, no input is required. To overcome initial energy loss, $| A \beta |$ is adjusted slightly greater than 1, and the circuit then stabilizes to achieve $| A \beta | = 1$, producing sustained oscillations.

Types of Oscillators

Oscillators are broadly classified into two types based on the nature of the output signal:

1. Sinusoidal
2. Non-Sinusoidal

• Sinusoidal Oscillators:

  Oscillators that generate a sinusoidal wave (either sine or cosine) as output are called sinusoidal oscillators. Examples include:

  • RC Oscillators (made with combinations of resistors and capacitors)
  • LC Oscillators (made with combinations of inductors and capacitors)
  • Crystal Oscillators

• Non-Sinusoidal Oscillators:

  Oscillators that generate a non-sinusoidal wave (such as a square wave or triangular wave) as output are called non-sinusoidal oscillators. Examples include:

  • Relaxation Oscillators
  • Multivibrators