Wien Bridge Oscillator

The Wien bridge oscillator is an RC oscillator that uses a Wien bridge circuit as its feedback network.

• The amplifier used in this oscillator is a non-inverting amplifier, which does not introduce any phase shift.
• The feedback network, a Wien bridge circuit, also does not introduce any phase shift.
• Therefore, the phase shift around a loop in a Wien bridge oscillator is $0^\circ$.

The figure below shows the basic circuit of the Wien bridge oscillator.

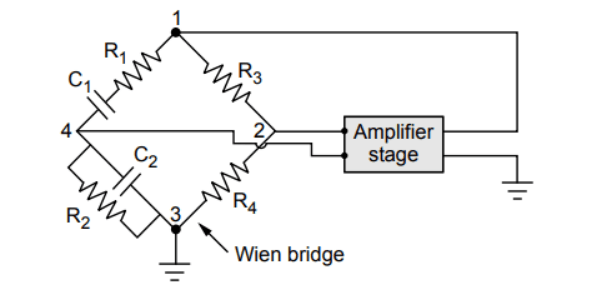
In this setup:

• The output of the amplifier is applied between terminals 1 and 3, while the amplifier is powered from terminals 2 and 4, which is the output of the feedback network.

Derivation of Frequency

The figure below illustrates the feedback network of the Wien bridge oscillator.

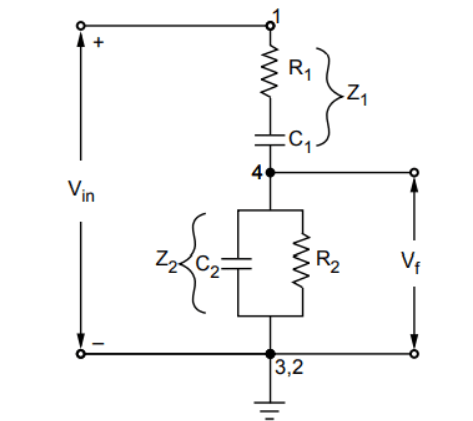
• The two arms of the feedback network are $R_1$, $C_1$ (in series) and $R_2$, $C_2$ (in parallel). These arms are frequency-sensitive and are therefore the focus of this analysis.

• The input to the feedback network is $V_{in}$, applied between terminals 1 and 3, which is the amplifier output.

• The output of the feedback network is $V_f$, taken from terminals 2 and 4.

• This network is also known as a lead-lag network.

  • $Z_1 = R_1 + \frac{1}{j\omega C_1} = \frac{R_1 j\omega C_1 + 1}{j\omega C_1}$
  • $Z_2 = R_2 \parallel \frac{1}{j\omega C_2} = \frac{R_2 \cdot \frac{1}{j\omega C_2}}{R_2 + \frac{1}{j\omega C_2}} = \frac{R_2}{1 + j\omega R_2 C_2}$

• The voltage $V_f$ across $Z_2$ is due to the current $I = \frac{V_{in}}{Z_1 + Z_2}$.

  $\therefore \; \; \; \; \; \; V_f = I Z_2 = \frac{Z_2}{Z_1 + Z_2} V_{in} \quad \text{i.e.} \quad \beta = \frac{V_f}{V_{in}} = \frac{Z_2}{Z_1 + Z_2}$

Using the expressions for $Z_1$ and $Z_2$ and simplifying:

$\beta = \frac{j\omega R_2 C_1}{(1 - \omega^2 R_1 R_2 C_1 C_2) + j\omega (R_1 C_1 + R_2 C_1)}$

Rationalizing and simplifying:

$\beta = \frac{\omega^2 C_1 R_2 (R_1 C_1 + R_2 C_2 + R_1 C_2) + j\omega C_1 R_2 (1 - \omega^2 R_1 R_2 C_1 C_2)}{(1 - \omega^2 R_1 R_2 C_1 C_2)^2 + \omega^2 (R_1 C_1 + R_2 C_1 + R_2 C_2)^2}$

$\quad \text{(i)}$

• To achieve zero phase shift, the imaginary part of the above equation must be zero:

  $\therefore \; \; \; \; \; \; \omega (1 - \omega^2 R_1 R_2 C_1 C_2) = 0$ but $\omega$ cannot be zero,

  $\therefore \; \; \; \; \; \; \omega^2 = \frac{1}{R_1 R_2 C_1 C_2} \quad \text{i.e.} \quad \omega = \frac{1}{\sqrt{R_1 R_2 C_1 C_2}}$

  $f = \frac{1}{2\pi \sqrt{R_1 R_2 C_1 C_2}} \text{ Hz}$

• In practice, if $R_1 = R_2 = R$ and $C_1 = C_2 = C$, then:

  $f = \frac{1}{2\pi RC} \text{ Hz}$

Using $\omega = \frac{1}{RC}$ in equation (i), we get the magnitude of the feedback network as:

$\beta = \frac{3}{0 + \frac{1}{(RC)^2} \cdot (3RC)^2} = \frac{3}{9} = \frac{1}{3}$

• For sustained oscillations, $|A\beta| \geq 1$, hence $|A| \geq 3$ for the Wien bridge oscillator.

• Thus, the gain of the amplifier stage must be at least 3 to ensure sustained oscillations.

• If $R_1 \neq R_2$ and $C_1 \neq C_2$, then using $\omega = \frac{1}{\sqrt{R_1 R_2 C_1 C_2}}$ in equation (i), we get:

  $\beta = \frac{C_1 R_2}{R_1 C_1 + R_2 C_2 + C_1 R_2}$

  and

  $A \geq \frac{R_1 C_1 + R_2 C_2 + C_1 R_2}{C_1 R_2}$

Advantages of the Wien Bridge Oscillator

• By mounting the two capacitors on a common shaft and varying their values, the frequency can be adjusted as needed.
• Due to the use of a two-stage amplifier, the gain is high.
• The stability is high.
• It provides stable, low-distortion sinusoidal output.
• The frequency range can be easily selected using decade resistance boxes.
• The circuit is straightforward to design and provides a constant output.

Disadvantages of the Wien Bridge Oscillator

• It cannot generate very high frequencies.
• The circuit requires two transistors and a considerable number of other components.
• The maximum frequency is limited by the amplitude and phase shift characteristics of the amplifiers.