Number Systems
A number system is a mathematical method for representing numbers. It uses arithmetic operations to express every number uniquely. To represent a number, it requires a base, also known as the radix.
In simple terms, a number system is a way of writing numbers using digits or symbols in a logical manner. A numeral system provides a useful set of numbers, reflects the arithmetic and algebraic structure of numbers, and offers a standard method of representation.
In the decimal number system, digits from 0 to 9 are used to form all numbers. With these digits, an infinite set of numbers can be created. For example: 156, 3907, 3456, 1298, 784859, etc. In addition to digits, alphabets like A, B, C, D, E, and F are used in the hexadecimal number system to represent different numbers.
Types of Number Systems
There are four common types of number systems based on the base or radix:
- Decimal number system (Base 10)
- Binary number system (Base 2)
- Octal number system (Base 8)
- Hexadecimal number system (Base 16)
1. Decimal Number System (Base 10)
The decimal number system has a base value of 10. It is also known as the base-10 number system, which includes 10 symbols: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. The position of each digit has a weight that is a power of 10.
This system plays a vital role in the development of science and technology. It is a positional number system where the value of each digit is determined by its position (or weight) in the number.
Each position in the decimal system is 10 times more significant than the previous position. The value of a decimal number is determined by multiplying each digit by the value of its position and then adding the products.
Example 1: The number 3254 is interpreted as:
- The digit 4 is in the ones place:
- The digit 5 is in the tens place:
- The digit 2 is in the hundreds place:
- The digit 3 is in the thousands place:
Thus,
Example 2: The number 2020.50 is interpreted as:
- The digit 0 is in the ones place:
- The digit 2 is in the tens place:
- The digit 0 is in the hundreds place:
- The digit 2 is in the thousands place:
For the decimal part:
- The digit 5 is in the tenths place:
- The digit 0 is in the hundredths place:
Putting it all together:
Advantages of the Decimal Number System (Base 10)
- Easy to understand and widely used in daily life.
- Basic operations like addition, subtraction, multiplication, and division are straightforward.
- Convenient for representing fractions using a decimal point.
- Easy to read and interpret for most people.
Disadvantages of the Decimal Number System (Base 10)
- Digital systems rely on binary (Base 2), requiring conversions between decimal and binary.
- Decimal is less efficient for computation compared to binary or hexadecimal in computing systems.
- More space and time are consumed in digital operations.
2. Binary Number System (Base 2)
The binary number system is used to represent numbers using only two symbols, “0” and “1”. The word "binary" comes from "bi," meaning two. This system is essential for computers because it uses only two states: 0 and 1.
In computers, these two states are represented by the presence or absence of current in transistors. When current passes through, the computer reads “1”; when there is no current, it reads “0”. Each binary digit is called a “bit.”
Example: The binary number 1011 is interpreted as:
- The rightmost digit (1) is in the place:
- The next digit (1) is in the place:
- The next digit (0) is in the place:
- The leftmost digit (1) is in the place:
Thus,
Advantages of the Binary System
- It is the native language of computers, ideal for electronic circuits.
- With only two digits, it simplifies representation in physical devices using on/off states.
- Binary states (0 and 1) are less prone to errors in digital systems.
Disadvantages of the Binary System
- Binary representations are longer than decimal or hexadecimal numbers, making them harder to read.
- Not as intuitive or readable for humans, requiring conversions for everyday use.
3. Octal Number System (Base 8)
The octal number system uses a base of 8 and eight symbols: 0, 1, 2, 3, 4, 5, 6, and 7. For example, , , , etc., are octal numbers. It is commonly used in computer programming, where each octal digit corresponds to three binary digits.
| Octal Numbers | Binary Equivalent |
|---|---|
| 0 | 000 |
| 1 | 001 |
| 2 | 010 |
| 3 | 011 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
Example: The octal number 345 is interpreted as:
- The rightmost digit (5) is in the place:
- The next digit (4) is in the place:
- The leftmost digit (3) is in the place:
Thus,
Advantages of the Octal System
- More compact than binary numbers, making them easier to read and write.
- Simplifies operations for certain digital systems.
- Octal arithmetic is simpler than hexadecimal arithmetic.
Disadvantages of the Octal System
- Largely replaced by hexadecimal in modern computing, which is more compact and easier to interpret.
- Less intuitive for people compared to decimal.
4. Hexadecimal Number System (Base 16)
The hexadecimal system has a base of 16 and includes 16 symbols: the numbers 0-9 and the letters A-F, with A representing 10, B representing 11, and so on. This system is widely used in computing and digital electronics.
| Hexadecimal | Decimal | Binary Equivalent |
|---|---|---|
| 0 | 0 | 0000 |
| 1 | 1 | 0001 |
| 2 | 2 | 0010 |
| 3 | 3 | 0011 |
| 4 | 4 | 0100 |
| 5 | 5 | 0101 |
| 6 | 6 | 0110 |
| 7 | 7 | 0111 |
| 8 | 8 | 1000 |
| 9 | 9 | 1001 |
| A | 10 | 1010 |
| B | 11 | 1011 |
| C | 12 | 1100 |
| D | 13 | 1101 |
| E | 14 | 1110 |
| F | 15 | 1111 |
Example: The hexadecimal number 2F3 is interpreted as:
- The rightmost digit (3) is in the place:
- The next digit (F) is in the place. Since F represents 15:
- The leftmost digit (2) is in the place:
Thus,
Advantages of the Hexadecimal System
- Provides a more compact representation of large binary numbers.
- Easy to convert between binary and hexadecimal.
- Commonly used in programming and debugging.
Disadvantages of the Hexadecimal System
- Less intuitive for people unfamiliar with it.
- Not widely used outside specialized fields like computing and electronics.
Conversions and Code
In electronics, "conversions and codes" refer to the processes and standards used to represent, convert, and interpret numerical values in various formats.
Conversions
-
Number Base Conversions:
-
Binary to Decimal: Converting binary numbers (base-2) to decimal numbers (base-10) involves interpreting binary digits using powers of 2.
-
Decimal to Binary: Converting decimal numbers to binary involves dividing the decimal number by 2 repeatedly and recording remainders.
-
Binary to Octal: Binary numbers can be grouped into sets of three bits to convert to octal (base-8).
-
Binary to Hexadecimal: Binary numbers can be grouped into sets of four bits to convert to hexadecimal (base-16).
-
Octal to Decimal: Each digit in an octal number is multiplied by the power of 8 corresponding to its position and summed.
-
Hexadecimal to Decimal: Each digit in a hexadecimal number is converted to decimal, multiplied by the power of 16 corresponding to its position, and summed.
-
-
Analog-to-Digital (A/D) and Digital-to-Analog (D/A) Conversions:
-
Analog-to-Digital Conversion: This process converts continuous analog signals into discrete digital numbers. It's used in digital systems to process analog inputs, such as sound or temperature.
-
Digital-to-Analog Conversion: This process converts digital signals into analog signals. It's used to produce analog outputs from digital data, such as in audio playback systems.
-
-
Signal Conversion:
-
Frequency Conversion: Changing the frequency of a signal, commonly used in communication systems for modulation and demodulation.
-
Voltage Level Conversion: Adjusting the voltage levels of signals, such as in interfacing different logic levels in digital circuits.
-
Codes
-
Binary Code:
-
Binary Coded Decimal (BCD): A binary-encoded representation of integer values where each decimal digit is represented by its own binary sequence.
- It is a form of binary encoding where each digit in a decimal number is represented in the form of bits.
- This encoding can be done in either 4-bit or 8-bit (usually 4-bit is preferred).
- It is a fast and efficient system that converts the decimal numbers into binary numbers as compared to the existing binary system.
- These are generally used in digital displays where is the manipulation of data is quite a task.
- Thus BCD plays an important role here because the manipulation is done treating each digit as a separate single sub-circuit.
Example: Convert in BCD:
thus, BCD becomes :
This is how decimal numbers are converted to their equivalent BCDs.
-
It is noticeable that the BCD is nothing more than a binary representation of each digit of a decimal number.
-
It cannot be ignored that the BCD representation of the given decimal number uses extra bits, which makes it heavy-weighted.
-
Gray Code: A binary numeral system where two successive values differ in only one bit, useful in error correction and digital encoders. The binary numeral system is ordered in the reflected binary code, also known as the Gray code, so that two subsequent values only differ in one bit (binary digit). In the typical sequence of binary numbers produced by the hardware that could provide an error or ambiguity during the change from one number to the next, gray codes are highly helpful.
Characteristics and Properties of Gray Code::
- Single Bit Change: Gray code only allows for one bit to change when changing from one value to another. Because there is less ambiguity when changing values, this feature lessens the possibility of errors and glitches in digital systems.
- Reflection Property: A straightforward way for creating the Gray Code sequence entails reflecting the current sequence before prefixing the new sequence with a new bit. For instance, start with a 2-bit Gray Code sequence and reflect it to make a 3-bit Gray Code sequence. The single-bit change property is upheld by the reflection property, which also makes sure the sequence is cyclic.
-
-
Error Detection and Correction Codes:
-
Parity Bit: A simple error detection scheme that adds a single bit to data to make the number of set bits either even or odd. A parity bit is an extra bit that is added to the message bits or data-word bits on the sender side. Data-word bits along with parity bits is called a codeword. The parity bit is added to the message bits on the sender side, to help in error detection at the receiver side. There are two parity systems – even and odd parity checks.
-
Even Parity: Total number of 1’s in the given data bit should be even. So if the total number of 1’s in the data bit is odd then a single 1 will be appended to make total number of 1’s even else 0 will be appended(if total number of 1’s are already even). Hence, if any error occurs, the parity check circuit will detect it at the receiver’s end.
-
Odd Parity: In odd parity system, if the total number of 1’s in the given binary string (or data bits) are even then 1 is appended to make the total count of 1’s as odd else 0 is appended. The receiver knows that whether sender is an odd parity generator or even parity generator. Suppose if sender is an odd parity generator then there must be an odd number of 1’s in received binary string. If an error occurs to a single bit that is either bit is changed to 1 to 0 or 0 to 1, received binary bit will have an even number of 1’s which will indicate an error.
-
-
Hamming Code: A method of error detection and correction that adds redundant bits to detect and correct single-bit errors. the source encodes the message by inserting redundant bits within the message. These redundant bits are extra bits that are generated and inserted at specific positions in the message itself to enable error detection and correction. When the destination receives this message, it performs recalculations to detect errors and find the bit position that has error.
-
Conversion of Bases (Decimal, Binary, Octal, and Hexadecimal Numbers)
A number in base or radix can be expressed as:
In this notation, to represent the integer part, followed by a radix point, with to representing the fractional part.
- = Most Significant Bit (MSB)
- = Least Significant Bit (LSB)
- Decimal to Binary Number System
- Binary to Decimal Number System
- Decimal to Octal Number System
- Octal to Decimal Number System
- Hexadecimal to Binary Number System
- Binary to Hexadecimal Number System
- Binary to Octal Number System
1. Decimal to Binary Number System:
To convert a decimal number to binary, start by dividing the decimal number by 2. Write down the remainder from bottom to top; this will give you the binary representation of the decimal number. If the number contains a fractional part, multiply the fractional part by 2.
Example: Convert to Binary:
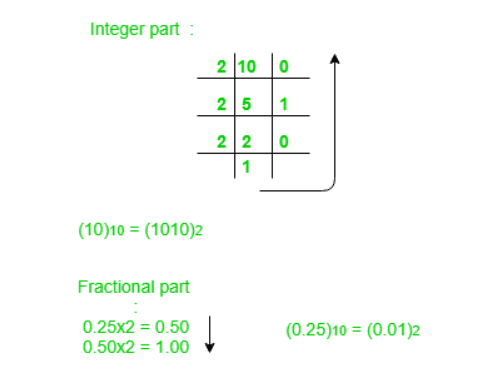
Keep multiplying the fractional part by 2 until the decimal part becomes .
Answer:
2. Binary to Decimal Number System:
To convert a binary number to decimal, multiply each digit of the number by raised to the power of its position, starting from the rightmost digit. If the number contains a fractional part, divide it by raised to the negative exponent corresponding to its position.
Example: Convert to Decimal:
Answer:
3. Decimal to Octal Number System:
To convert a decimal number to octal, follow these steps:
-
Divide the Decimal Number by 8: Start by dividing the decimal number by . Record the quotient and the remainder.
-
Continue Dividing the Quotient: Take the quotient from the first division and divide it by again.
-
Collect the Remainders: The octal representation is constructed from the remainders obtained, starting from the last remainder collected to the first.
- From the second division:
- From the first division:
-
Construct the Octal Representation: Thus, when reading from bottom to top, we have:
-
Handle the Fractional Part: For the fractional part, multiply it by .
Keep multiplying the fractional part by until you get .
Answer:
4. Octal to Decimal Number System:
To convert an octal number to decimal, multiply each digit of the number by raised to the power of its position, starting from the rightmost digit. For the fractional part, divide it by raised to the negative exponent corresponding to its position.
Example: Convert to Decimal:
Answer:
5. Hexadecimal to Binary Number System:
To convert from hexadecimal to binary, write down the 4-bit binary equivalent of each hexadecimal digit.
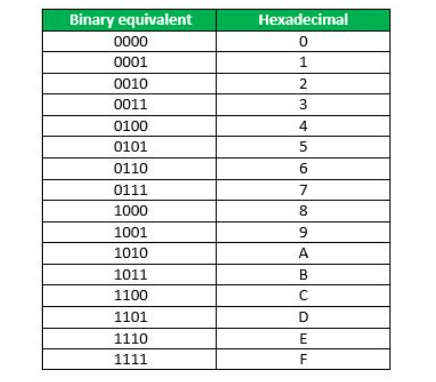
Example: Convert to Binary:
6. Binary to Hexadecimal Number System:
To convert a binary number to hexadecimal, follow these steps:
-
Group the Bits: Starting from the right end, group the binary digits into sets of .
Example: For :
-
Convert Each Group: Write down the equivalent hexadecimal digit for each -bit group.
-
Combine the Hexadecimal Digits:
7. Binary to Octal Number System:
To convert a binary number to octal, follow these steps:
-
Group the Bits: Starting from the right end, group the binary digits into sets of .
Example: For :
-
Convert Each Group: Write down the equivalent octal digit for each -bit group.
-
Combine the Octal Digits:
Addition and Subtraction
Addition using 1's complement
When adding two binary numbers, three different cases may arise:
Case 1: Addition of a positive number with a negative number where the positive number has a greater magnitude.
First, calculate the 1's complement of the given negative number, then sum it with the positive number. If an end-around carry (a carry out of the most significant bit) is produced, add it to the least significant bit (LSB).
Example: 1101 and -1001:
-
First, find the 1's complement of the negative number . To find the 1's complement, change all 0s to 1s and all 1s to 0s. The 1's complement of is .
-
Now, add both numbers: :
-
The addition yields an end-around carry of 1. Add this carry to the LSB of :
Case 2: Addition of a positive value with a negative value when the negative number has a higher magnitude.
Calculate the 1's complement of the negative value and sum it with the positive number. If there is no end-around carry, take the 1's complement of the result to find the final answer.
Example: 1101 and -1110:
-
First, find the 1's complement of the negative number . The 1's complement of is .
-
Now, add both numbers: :
-
Take the 1's complement of the result to get the final answer. The 1's complement of is , and we prepend a negative sign to indicate it is a negative number.
Case 3: Addition of two negative numbers.
First, find the 1's complement of both negative numbers, then add the complements. This will always yield an end-around carry, which should be added to the LSB. Finally, take the 1's complement of the result to get the final answer.
Example: -1101 and -1110 in a five-bit register:
-
First, find the 1's complement of the negative numbers and . The 1's complement of is , and for , it is .
-
Now, add the complement numbers: :
-
The addition produces an end-around carry of 1. Add this carry to the LSB of :
-
Finally, find the 1's complement of the result for the final answer. The 1's complement of is , and we add a negative sign before the number to indicate it is negative.
Subtraction using 1's complement
To subtract two binary numbers using 1's complement, follow these steps:
- First, find the 1's complement of the subtrahend (the number to be subtracted).
- Next, add the complement to the minuend (the number from which another number is subtracted).
- If a carry is generated, add it to the LSB. If there is no carry, take the 1's complement of the result to indicate that it is negative.
Example 1: :
-
Find the 1's complement of the subtrahend , which is . Now, add:
-
The result contains a carry bit of 1, so we add this to the LSB of :
Example 2: :
-
Find the 1's complement of the subtrahend , which is . Now, add:
-
This result does not generate a carry bit. So, take the 1's complement of :
This indicates a negative number and is the final answer.
Addition using 2's complement
When adding two binary numbers using 2's complement, three cases may arise:
Case 1: Addition of a positive number with a negative number when the positive number has a greater magnitude.
First, calculate the 2's complement of the given negative number and then add it to the positive number. If an end-around carry is produced, discard the carry bit; the remaining bits are the final result.
Example: and :
-
Find the 2's complement of the negative number . To find the 2's complement, first get the 1's complement (), then add 1:
-
Add both numbers: :
-
The addition yields an end-around carry of 1, which we discard. The result is .
Case 2: Adding a positive value with a negative value when the negative number has a higher magnitude.
Add the positive number with the 2's complement of the negative number. If no end-around carry is generated, take the 2's complement of the result to obtain the final answer.
Example: and :
-
Find the 2's complement of . The 1's complement is ; adding 1 gives:
-
Add :
-
Take the 2's complement of for the final answer. The 2's complement of is , and we prepend a negative sign.
Case 3: Addition of two negative numbers.
First, find the 2's complement of both negative numbers, then add the complements. There will always be an end-around carry, which is added to the LSB. To get the final result, take the 2's complement of the result.
Example: and in a five-bit register:
-
Find the 2's complement of and . The 1's complements are and , respectively. Adding 1 gives:
- becomes
- becomes
-
Now add :
-
An end-around carry of 1 is generated. Discard this carry; the final result is the 2's complement of :
-
Prepend a negative sign to indicate that it is a negative number.
Subtraction using 2's complement
To subtract two binary numbers using 2's complement, follow these steps:
- First, find the 2's complement of the subtrahend.
- Add this complement to the minuend.
- If a carry is produced, discard it; the result is positive. If there is no carry, take the 2's complement of the result to indicate it is negative.
Example 1: :
-
The 2's complement of is . Add:
-
An end-around carry of 1 is generated, which we discard. The final result is , a positive number.
Example 2: :
-
The 2's complement of is . Add:
-
No carry is generated, so take the 2's complement of :
This indicates a negative number and is the final answer.
Boolean Algebra
The logical symbols 0 and 1 are used to represent digital inputs or outputs. The symbols "1" and "0" can also be used for a permanently open and closed digital circuit, respectively. A digital circuit can be composed of several logic gates. To perform logical operations with the minimum number of logic gates, a set of rules was invented, known as the Laws of Boolean Algebra. These rules are used to reduce the number of logic gates needed for performing logical operations.
Rules in Boolean Algebra
- Only two values (1 for high and 0 for low) are possible for the variables used in Boolean algebra.
- The overbar (-) is used to represent the complement of a variable. Therefore, the complement of variable C is represented as .
- The plus (+) operator is used to represent the OR operation between the variables.
- The dot (·) operator is used to represent the AND operation between the variables.
Properties of Boolean Algebra
The following properties are essential in Boolean algebra:
-
Annulment Law: When a variable is ANDed with 0, it results in 0; when a variable is ORed with 1, it results in 1, i.e.,
-
Identity Law: When a variable is ANDed with 1 and ORed with 0, the variable remains unchanged, i.e.,
-
Idempotent Law: When a variable is ANDed and ORed with itself, the variable remains unchanged, i.e.,
-
Complement Law: When a variable is ANDed with its complement, it results in 0, and when it is ORed with its complement, it results in 1.
-
Double Negation Law: This law states that when a variable has two negations, the symbol gets removed, yielding the original variable.
-
Commutative Law: This law states that the order of the variables does not matter in operations.
-
Associative Law: This law states that the operation can be performed in any order when the variables have the same priority with respect to AND and OR.
-
Distributive Law: This law allows the expansion of expressions by distributing one operation over another.
-
Absorption Law: This law allows for the simplification of expressions involving similar variables.
Advantages of Boolean Algebra
-
Simplification: By using Boolean algebra, we can decompose complex logic into its basic simple form without changing the resultant value. This minimizes the complexity of logic circuits, reducing the number of required logic gates and overall cost.
-
Formalism: Boolean algebra allows for the analysis of logical relationships, facilitating accurate modeling and manipulation of logical operations.
-
Standardization: Boolean algebra ensures consistency and uniformity across various fields and applications.
Disadvantages of Boolean Algebra
-
Complexity in Real-World Problems: Boolean algebra only takes two values (0 and 1), but many real-world applications require multi-valued, fractional, or higher-order values.
-
Steep Learning Curve: Implementing Boolean algebra requires extensive training due to its unique rules, theorems, and abstract nature.