Transistor Biasing and Bias Stabilization

Operating Point

The proper flow of zero signal collector current and the maintenance of proper collector-emitter voltage during the passage of a signal is known as Transistor Biasing. The circuit that provides transistor biasing is called a Biasing Circuit.

Need for DC biasing

If a signal of very small voltage is applied to the input of a BJT, it cannot be amplified. This is because, for a BJT to amplify a signal, two conditions must be met:

• The input voltage should exceed the cut-in voltage for the transistor to be ON.
• The BJT should be in the active region to operate as an amplifier.

If appropriate DC voltages and currents are supplied to the BJT by external sources, ensuring the BJT operates in the active region while superimposing the AC signals to be amplified, this problem can be avoided. The given DC voltage and currents are chosen so that the transistor remains in the active region throughout the entire input AC cycle. Hence, DC biasing is necessary.

The below figure shows a transistor amplifier that is provided with DC biasing in both input and output circuits.

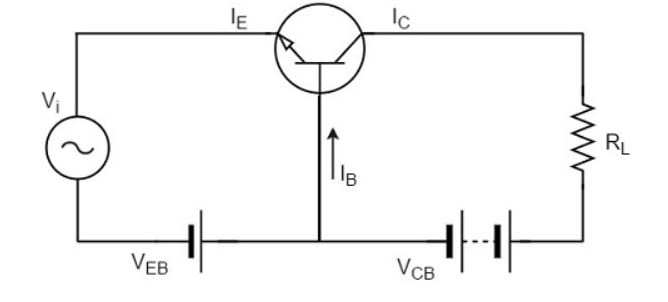
Operating Point

When a line is drawn connecting the saturation and cutoff points, it is called a Load Line. This line, when drawn over the output characteristic curve, intersects at a point known as the Operating Point.

This operating point is also called the quiescent point or simply the Q-point. There can be many such intersecting points, but the Q-point is selected in such a way that, irrespective of the AC signal swing, the transistor remains in the active region.

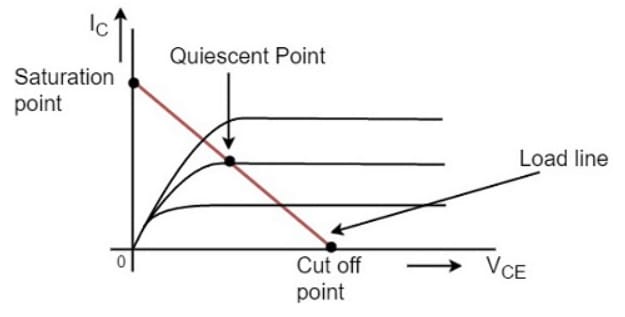
The operating point should not get disturbed, as it must remain stable to achieve faithful amplification. Hence, the quiescent point or Q-point is the value where Faithful Amplification is achieved.

Factors affecting the operating point

The main factor that affects the operating point is temperature. The operating point shifts due to changes in temperature.

As temperature increases, the values of $I_{CE}$, $\beta$, and $V_{BE}$ are affected.

So, the main problem affecting the operating point is temperature. Hence, the operating point should be made independent of temperature to achieve stability. To achieve this, biasing circuits are introduced.

Stability Factor

The process of making the operating point independent of temperature changes or variations in transistor parameters is known as Stabilization.

Once stabilization is achieved, the values of $I_C$ and $V_{CE}$ become independent of temperature variations or transistor replacement. A good biasing circuit helps in the stabilization of the operating point.

Need for Stabilization

Stabilization of the operating point is necessary due to the following reasons:

• Temperature dependence of $I_C$
• Individual variations
• Thermal runaway

1. Temperature Dependence of $I_C$

   The expression for collector current $I_C$ is:

   $I_C = \beta I_B + I_{CEO} = \beta I_B + (\beta + 1)I_{CBO}$

   The collector leakage current $I_{CBO}$ is greatly influenced by temperature variations. To counter this, the biasing conditions are set so that the zero signal collector current $I_C = 1 mA$. Therefore, the operating point needs to be stabilized, i.e., it is necessary to keep $I_C$ constant.

2. Individual Variations

   As the value of $\beta$ and the value of $V_{BE}$ are not the same for every transistor, whenever a transistor is replaced, the operating point tends to change. Hence, it is necessary to stabilize the operating point.

3. Thermal Runaway

   The expression for collector current $I_C$ is:

   $I_C = \beta I_B + I_{CEO} = \beta I_B + (\beta + 1)I_{CBO}$

   The flow of collector current, along with the collector leakage current, causes heat dissipation. If the operating point is not stabilized, a cumulative effect occurs, increasing this heat dissipation.

   The self-destruction of such an unstabilized transistor is known as Thermal Runaway.

   To avoid thermal runaway and the destruction of the transistor, it is necessary to stabilize the operating point, i.e., to keep $I_C$ constant.

Stability Factor

It is understood that $I_C$ should be kept constant despite variations in $I_{CBO}$ or $I_{CO}$. The extent to which a biasing circuit is successful in maintaining this is measured by the Stability Factor, denoted by $S$.

By definition, the rate of change of collector current $I_C$ with respect to the collector leakage current $I_{CO}$ at constant $\beta$ and $I_B$ is called the Stability Factor.

$$S = \frac{dI_C}{dI_{CO}}$$

at constant $I_B$ and $\beta$

Hence, we can understand that any change in collector leakage current greatly affects the collector current. The stability factor should be as low as possible so that the collector current doesn’t get affected. $S=1$ is the ideal value.

The general expression of the stability factor for a CE configuration can be obtained as follows:

$$I_C = \beta I_B + (\beta + 1)I_{CO}$$

Differentiating the above expression with respect to $I_C$, we get:

$$1 = \beta \frac{dI_B}{dI_C} + (\beta + 1)\frac{dI_{CO}}{dI_C}$$

Or:

$$1 = \beta \frac{dI_B}{dI_C} + \frac{(\beta + 1)}{S}$$

Since:

$$\frac{dI_{CO}}{dI_C} = \frac{1}{S}$$

Or:

$$S = \frac{\beta + 1}{1− \beta (\frac{dI_B}{dI_C})}$$

Hence the stability factor $S$ depends on $\beta$, $I_B$ and $I_C$.

Methods of Transistor Biasing

Biasing in transistor circuits is typically done using two DC sources: $V_{BB}$ and $V_{CC}$. However, it is more economical to minimize the number of DC sources to one, which also simplifies the circuit.

The commonly used methods of transistor biasing are:

• Fixed bias circuit (Single Base Resistor Biasing) or base bias
• Collector-to-base bias
• Biasing with collector feedback resistor
• Voltage-divider bias circuit (V.D.B) or self-bias
• Emitter bias or modified fixed bias circuit

All of these methods share the basic principle of obtaining the required value of $I_B$ and $I_C$ from $V_{CC}$ under zero signal conditions.

Fixed Bias Circuit (Single Base Resistor Biasing) or Base Bias

In this method, as the name implies, a resistor $R_B$ with high resistance is connected to the base. The required zero signal base current is provided by $V_{CC}$, which flows through $R_B$. The base-emitter junction is forward biased since the base is positive with respect to the emitter.

The required value of zero signal base current and, consequently, the collector current (since $I_C = \beta I_B$) can be achieved by selecting the appropriate value of the base resistor $R_B$. Therefore, it is necessary to determine the value of $R_B$. The figure below shows the base resistor method of biasing.

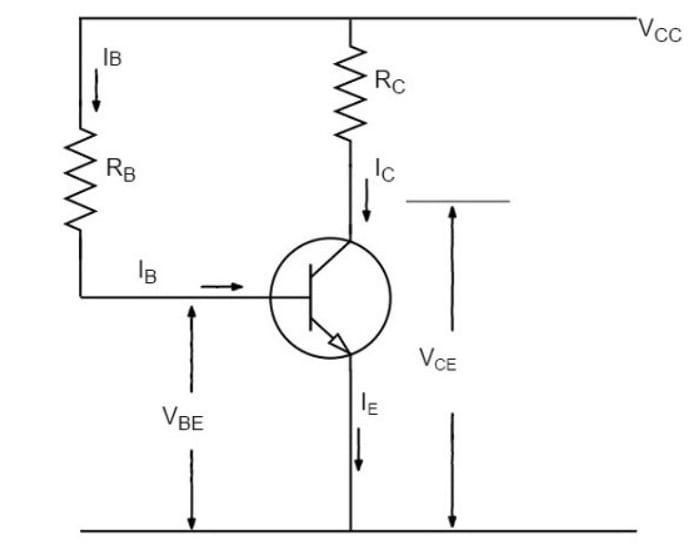
Let $I_C$ be the required zero signal collector current. Therefore:

$I_B = \frac{I_C}{\beta}$

Considering the closed circuit from $V_{CC}$ through the base, emitter, and ground, and applying Kirchhoff’s voltage law, we get:

$V_{CC} = I_B R_B + V_{BE}$

Or:

$I_B R_B = V_{CC} − V_{BE}$

Therefore:

$R_B = \frac{V_{CC} − V_{BE}}{I_B}$

Since $V_{BE}$ is generally quite small compared to $V_{CC}$, it can be neglected with minimal error. Then:

$R_B = \frac{V_{CC}}{I_B}$

We know that $V_{CC}$ is a fixed, known quantity, and $I_B$ is chosen at a suitable value. Since $R_B$ can be found directly, this method is called the fixed bias method.

Stability Factor

The stability factor $S$ is given by:

$S = \frac{\beta + 1}{1 − \beta\left(\frac{dI_B}{dI_C}\right)}$

In the fixed-bias method of biasing, $I_B$ is independent of $I_C$, so:

$\frac{dI_B}{dI_C} = 0$

Substituting this value into the equation, the stability factor becomes:

$S = \beta + 1$

Thus, the stability factor in a fixed bias circuit is $\beta + 1$, which means that $I_C$ changes $\beta + 1$ times as much as any change in $I_{CO}$.

Advantages:

• The circuit is simple.
• Only one resistor $R_B$ is required.
• Biasing conditions are easily set.
• There is no loading effect, as no resistor is present at the base-emitter junction.

Disadvantages:

• Stabilization is poor, as heat development cannot be controlled.
• The stability factor is very high, increasing the risk of thermal runaway.

Collector-to-Base Bias

The collector-to-base bias circuit is similar to the base bias circuit, except that the base resistor $R_B$ is connected to the collector rather than the $V_{CC}$ supply.

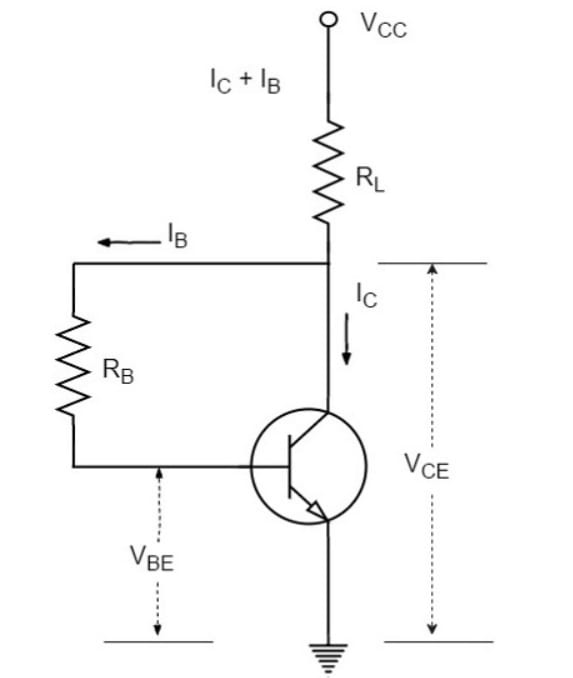
This circuit helps improve stability significantly. If the value of $I_C$ increases, the voltage across $R_L$ increases, which in turn reduces the base current $I_B$. This action compensates for the original increase in $I_C$.

The required value of $R_B$ needed to provide the zero signal collector current $I_C$ can be calculated as follows:

The voltage drop across $R_L$ will be:

$V_{R_L} = (I_C + I_B) R_L ≅ I_C R_L$

From the figure:

$I_C R_L + I_B R_B + V_{BE} = V_{CC}$

Or:

$I_B R_B = V_{CC} − V_{BE} − I_C R_L$

Therefore:

$R_B = \frac{V_{CC} − V_{BE} − I_C R_L}{I_B}$

Or:

$R_B = \frac{(V_{CC} − V_{BE} − I_C R_L) \beta}{I_C}$

Applying Kirchhoff's Voltage Law (KVL):

$(I_B + I_C) R_L + I_B R_B + V_{BE} = V_{CC}$

Or:

$I_B (R_L + R_B) + I_C R_L + V_{BE} = V_{CC}$

Therefore:

$I_B = \frac{V_{CC} − V_{BE} − I_C R_L}{R_L + R_B}$

Since $V_{BE}$ is almost independent of collector current, we get:

$\frac{dI_B}{dI_C} = − \frac{R_L}{R_L + R_B}$

We know that:

$S = \frac{1 +\beta}{1− \beta \left(\frac{dI_B}{dI_C}\right)}$

Therefore:

$S = \frac{1 + \beta}{1 + \beta \left(\frac{R_L}{R_L + R_B}\right)}$

This value is smaller than $(1 + \beta)$, which is obtained for the fixed bias circuit, indicating an improvement in stability.

This circuit provides negative feedback, which reduces the gain of the amplifier. Thus, the increased stability of the collector-to-base bias circuit is obtained at the cost of AC voltage gain.

Advantages of the Collector-to-Base Bias Circuit:

• Simple circuit design.
• Provides some stabilization of the operating point.
• Requires only one resistor at the base.
• Reduced sensitivity to transistor variations.
• Lower sensitivity to power supply changes.

Disadvantages of the Collector-to-Base Bias Circuit:

• Does not provide optimal stabilization, as the stability factor is high.
• Negative feedback reduces the gain of the amplifier.
• Dependency on component matching.
• More complex compared to fixed bias circuits.
• Limited use in certain applications with specific voltage requirements.

Biasing with Collector Feedback Resistor

In this method, the base resistor $R_B$ has one end connected to the base and the other to the collector, as the name implies. In this circuit, the zero signal base current is determined by $V_{CB}$ rather than by $V_{CC}$.

$V_{CB}$ forward-biases the base-emitter junction, causing base current $I_B$ to flow through $R_B$, which in turn causes the zero signal collector current to flow in the circuit. The figure below shows the biasing with a collector feedback resistor circuit.

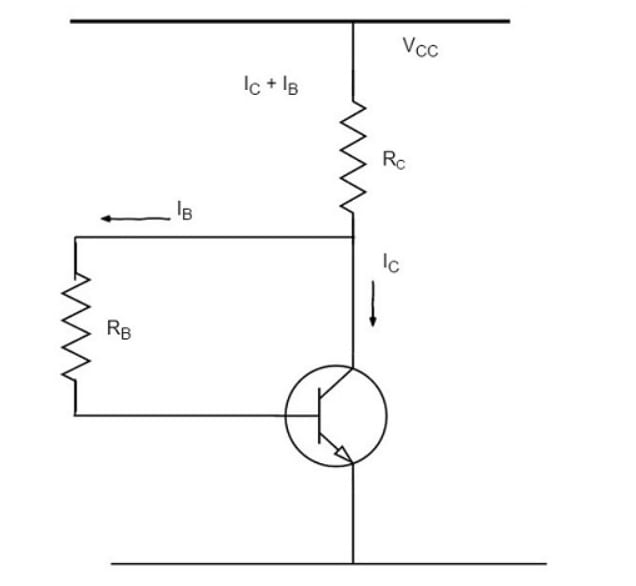
The required value of $R_B$ needed to provide the zero signal collector current $I_C$ can be determined as follows:

$V_{CC} = I_C R_C + I_B R_B + V_{BE}$

Or:

$R_B = \frac{V_{CC} − V_{BE} − I_C R_C}{I_B}$

$= \frac{V_{CC} − V_{BE}− \beta I_B R_C}{I_B}$

Since:

$I_C = \beta I_B$

Alternatively:

$V_{CE} = V_{BE} + V_{CB}$

Or:

$V_{CB} = V_{CE} − V_{BE}$

Since:

$R_B = \frac{V_{CB}}{I_B} = \frac{V_{CE} − V_{BE}}{I_B}$

Where:

$I_B = \frac{I_C}{\beta}$

Mathematically, the stability factor is:

$S < (\beta + 1)$

Therefore, this method provides better thermal stability than the fixed bias method.

The Q-point values for the circuit are:

$I_C = \frac{V_{CC} − V_{BE}}{R_B/\beta + R_C}$

$V_{CE} = V_{CC} − I_C R_C$

Advantages:

• The circuit is simple, requiring only one resistor.
• Provides some stabilization for lesser changes.

Disadvantages:

• The circuit does not provide strong stabilization.
• The circuit provides negative feedback, which reduces the gain.

Voltage-Divider Bias Circuit (V.D.B) or Self-Bias

Among all methods of providing biasing and stabilization, the voltage-divider bias method is the most commonly used. In this method, two resistors $R_1$ and $R_2$ are connected to $V_{CC}$ to provide biasing, while the resistor $R_E$ in the emitter provides stabilization.

The name "voltage divider" comes from the voltage divider formed by $R_1$ and $R_2$. The voltage drop across $R_2$ forward-biases the base-emitter junction, which causes the base current and hence the collector current to flow under zero signal conditions. The figure below shows the circuit of the voltage-divider bias method.

Suppose the current flowing through resistance $R_1$ is $I_1$. Since the base current $I_B$ is very small, it can be assumed with reasonable accuracy that the current flowing through $R_2$ is also $I_1$.

Collector Current, $I_C$:

From the circuit, it is evident that:

$I_1 = \frac{V_{CC}}{R_1 + R_2}$

Therefore, the voltage across resistance $R_2$ is:

$V_2 = \left(\frac{V_{CC}}{R_1 + R_2}\right) R_2$

Applying Kirchhoff’s Voltage Law (KVL) to the base circuit:

$V_2 = V_{BE} + V_E$

$V_2 = V_{BE} + I_E R_E$

$I_E = \frac{V_2 − V_{BE}}{R_E}$

Since $I_E ≈ I_C$:

$I_C = \frac{V_2 − V_{BE}}{R_E}$

From the above expression, it is evident that $I_C$ doesn’t depend on $\beta$. $V_{BE}$ is very small, so $I_C$ doesn’t get affected by $V_{BE}$ at all. Thus, $I_C$ in this circuit is almost independent of transistor parameters, and good stabilization is achieved.

Collector-Emitter Voltage, $V_{CE}$

Applying KVL to the collector side:

$V_{CC} = I_C R_C + V_{CE} + I_E R_E$

Since $I_E ≅ I_C$:

$= I_C R_C + V_{CE} + I_C R_E$

$= I_C(R_C + R_E) + V_{CE}$

Therefore:

$V_{CE} = V_{CC} − I_C (R_C + R_E)$

$R_E$ provides excellent stabilization in this circuit.

$V_2 = V_{BE} + I_C R_E$

Suppose there is a rise in temperature; the collector current $I_C$ increases, which causes the voltage drop across $R_E$ to increase. As the voltage drop across $R_2$ is $V_2$, which is independent of $I_C$, the value of $V_{BE}$ decreases. The reduced value of $I_B$ tends to restore $I_C$ to its original value.

Stability Factor

The equation for the Stability Factor of this circuit is obtained as:

Stability Factor:

$S = \frac{(\beta + 1)(R_0 + R_E)}{R_0 + R_E + \beta R_E}$

$= (\beta + 1) \times \frac{1 + \frac{R_0}{R_E}}{\beta + 1 + \frac{R_0}{R_E}}$

Where:

$R_0 = \frac{R_1 R_2}{R_1 + R_2}$

If the ratio $\frac{R_0}{R_E}$ is very small, then $\frac{R_0}{R_E}$ can be neglected compared to 1, and the stability factor becomes:

Stability Factor:

$S = (\beta + 1) \times \frac{1}{\beta + 1} = 1$

This is the smallest possible value of $S$ and leads to the maximum possible thermal stability.

Emitter Bias or Modified Fixed Bias Circuit

In this configuration, a resistor $R_E$ is added from the emitter to the ground terminal of the fixed bias circuit. This is done to improve the stability of the circuit.

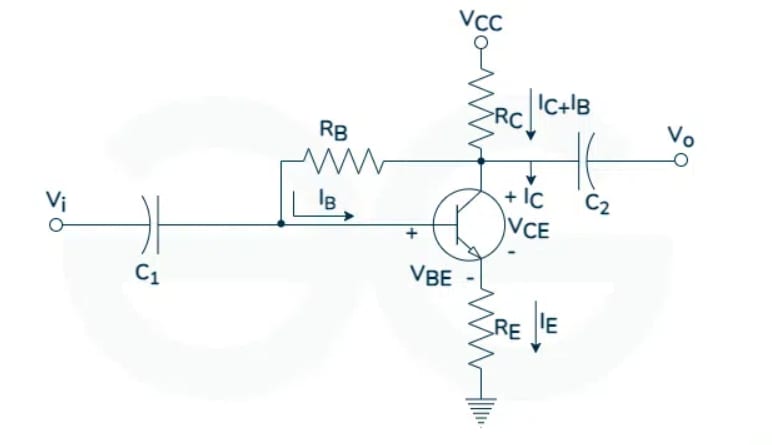
Base Circuit:

Applying KVL to this circuit:

$V_{CC} = I_B R_B + V_{BE} + I_E R_E$

But:

$I_E = I_B + I_C$

and:

$I_C = \beta I_B$

Substituting the value of $I_C$ into $I_E$, we get:

$I_E = I_B + \beta I_B$

Now, substituting the value of $I_E$ into $V_{CC}$:

$V_{CC} = I_B R_B + V_{BE} + (\beta I_B + I_B) R_E$

$= I_B(R_B + \beta R_E + R_E) + V_{BE}$

$\therefore I_B = \frac{(V_{CC} - V_{BE})}{(R_B + \beta R_E + R_E)}$

Collector Circuit:

Applying KVL to this circuit:

$V_{CC} = I_C R_C + V_{CE} + I_E R_E$

Since $I_E = I_B + I_C$:

$V_{CC} = I_C R_C + V_{CE} + (\beta I_B + I_B) R_E$

$V_{CE} = V_{CC} - I_B R_E - I_C (R_C + R_E)$

Where:

$I_C = \beta I_B$

$\therefore I_C = \beta \left[\frac{(V_{CC} - V_{BE})}{(R_B + \beta R_E + R_E)}\right]$

Advantages of the Modified Fixed Bias Circuit:

• The addition of the emitter resistor $R_E$ provides improved stability.
• It offers a high voltage gain.
• It is a simple circuit with enhanced stabilization.
• Reduced sensitivity to transistor variations.
• It strikes a balance between simplicity and performance.

Disadvantages of the Modified Fixed Bias Circuit:

• The operating point can be affected by changes in temperature.
• It requires the use of a dual polarity power supply.
• Limited voltage range.
• Potential issues with component matching.
• More complex than a simple fixed bias circuit.