Time Dilation

The word dilation means to lengthen. Consider two coordinate systems $F$ and $F'$ such that $F'$ is moving with velocity $v$ along the x-axis relative to $F$. Imagine a gun placed at the fixed position $(x', y', z')$ in the frame $F'$. Suppose it fires two shots at time intervals $t_1'$ and $t_2'$ measured by observer $O'$ in the frame $F'$.

Derivation

According to Classical Physics, time is an absolute quantity. But according to the Special Theory of Relativity, time is not an absolute quantity. It depends upon the motion of the frame of reference as we can see in Lorentz's transformation. The word dilation means to lengthen an interval of time.

Let us consider two observers in two different inertial frames moving with relative speed v comparable to speed of light. If they measure time with their clock, then both will say that their clock is running fine but the other observer's clock is running slow.

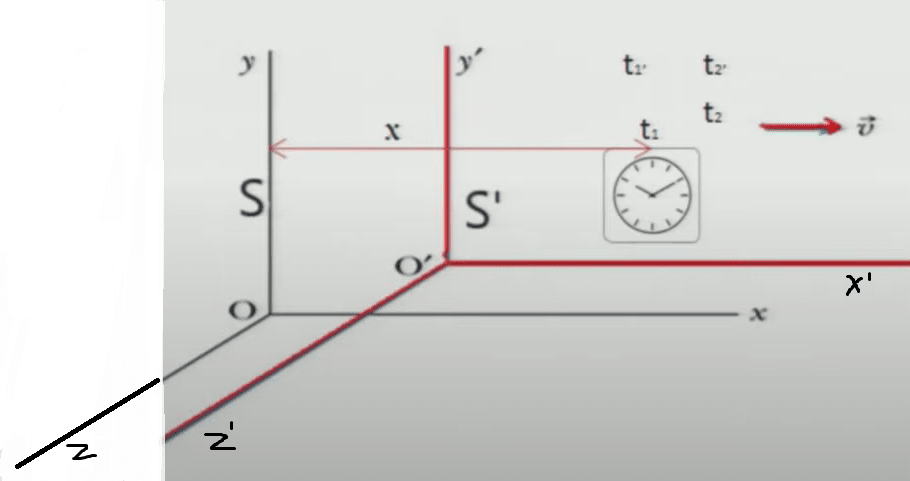
Let us consider two inertial frames $S$ and $S'$. Let $S$ is moving with relative speed $v$ with respect to $S$ in X direction. Let the observer in frame $S$ at position X, measures time interval as -

$\triangle t = t_2 - t_1$

The observer in frame $S'$ measures the time interval as -

$\triangle t' = t_2' - t_1'$

From Lorentz Transformations, we have:-

$t_1' = \frac{t_1 - \frac{xv}{c^2}}{\sqrt{1 - \frac{v^2}{c^2}}}$ $\; \; and \; \;$ $t_2' = \frac{t_2 - \frac{xv}{c^2}}{\sqrt{1 - \frac{v^2}{c^2}}}$

$\therefore \; \triangle t' = t_2' - t_1' = \frac{t_2 - \frac{xv}{c^2}}{\sqrt{1 - \frac{v^2}{c^2}}} - \frac{t_1 - \frac{xv}{c^2}}{\sqrt{1 - \frac{v^2}{c^2}}} =$

$\frac{t_2 - t_1}{\sqrt{1 - \frac{v^2}{c^2}}} = \frac{\triangle t}{\sqrt{1 - \frac{v^2}{c^2}}}$

Thus if v is much less than c, then $\triangle t' = \triangle t$. But then if v is close to c, then $\triangle t' > \triangle t$. This means that time interval in system $S'$ is greater than the time interval in frame S. This is known as time dilation.

Numericals on Time Dilation

Length Contraction

In classical mechanics, the length of an object is independent of the velocity of the moving observer relative to the object. However, on the basis of the theory of relativity, the length of an object depends upon the velocity of the observer with respect to the object.

Derivation

If we measure the length of anything moving relative to our frame, we find its length $L_o'$ to be smaller than the proper length $L_o$ that would be measured if the object were stationary. At relativistic speeds, Close to the speed of light, distances measured are not the same when measured by different observers.

Thus, according to Einstein's Theory of relativity, length contraction is the phenomenon in which the length of an object is measured to be shorter than its proper length measured in the rest frame. It is also known as Lorentz contraction and mainly noticeable when the inertial frame of reference moves with a substantial fraction of the speed of light.

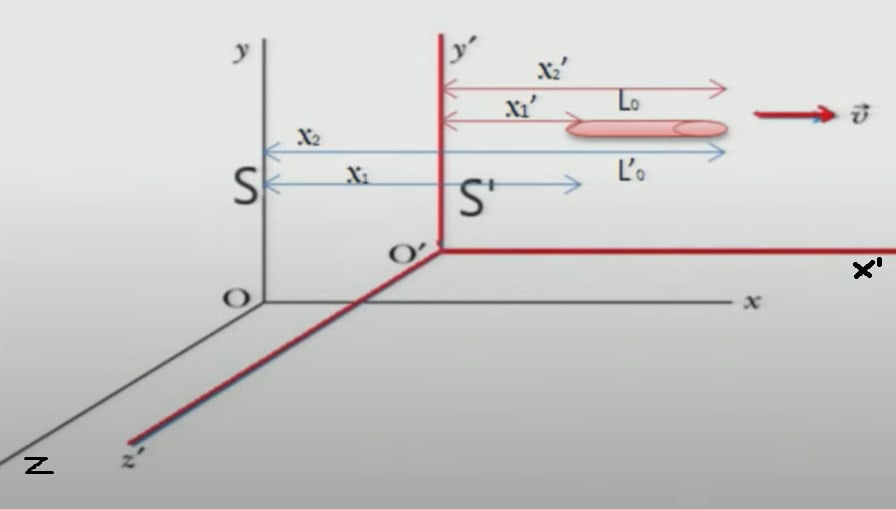
Let us consider two inertial frames $S$ and $S'$. Let $S'$ is moving with relative speed v with respect to $S$ in X direction. Let an observer in frame $S$, measures length of the rod as-

$L_o = x_2 - x_1$

Similarly, an observer in frame $S'$ will measure the length if the rod as :- $L_o' = x_2' - x_1'$

According to Lorentz transformations,

$x_2' = \frac{x_2-vt}{\sqrt{1 - \frac{v^2}{c^2}}}$ $\; \; and \; \;$ $x_1' = \frac{x_1-vt}{\sqrt{1 - \frac{v^2}{c^2}}}$

$\therefore \; L_o' = x_2' - x_1' = \frac{x_2-vt}{\sqrt{1 - \frac{v^2}{c^2}}} - \frac{x_1-vt}{\sqrt{1 - \frac{v^2}{c^2}}} =$

$\frac{x_2-x_1}{\sqrt{1 - \frac{v^2}{c^2}}} = \frac{L_o}{\sqrt{1 - \frac{v^2}{c^2}}}$

$\therefore \; L_o = L_o' \sqrt{1 - \frac{v^2}{c^2}}$

It means that the length of the rod moving with velocity $v$ relative to the observer is contracting by a factor, $\sqrt{1 - \frac{v^2}{c^2}}$ in the direction of the motion. When $v<<c \;$, $\; L_o' = L_o$, But when $v$ is comparable to $c$, then $L_o<L_o'$ . This is called as Length contraction.

Numericals On Length Contraction

Twin Paradox

The twin paradox is a thought experiment in physics that involves two identical twins. In the paradox, one twin travels at high speed into space and returns home to find that the twin who stayed on Earth has aged more.