Lorentz Transformation eq.s

Theory And Derivation of L T.

The Lorentz transformation is a mathematical description of how space and time coordinates are transformed between different inertial frames of reference that are moving relative to each other with constant velocity. It was developed to make the eq.s of electromagnetism compatible with the theory of relativity. Lorentz proposed "contracting" lengths in the direction of motion in order to explain the Michelson-Morley experiment.

It involves scaling space and time coordinates by a factor that depends on velocity, known as the Lorentz factor. This results in length contraction and time dilation between frames. Lorentz transformations are related to only the inertial frame of reference and coordinate a relationship between two frames in linear motion that move at a constant velocity with respect to each other, in the context of special theory of relativity.

Each coordinate in one frame is a linear function to the other frame and each parameter describes the direction, speed and orientation of the eq.s.

Lorentz Boost

A Lorentz boost is a transformation that changes between two inertial frames of reference that are in relative motion. It is a special case of the Lorentz transformation where the spatial coordinates are rotated.

When one frame is moving at a constant velocity with respect to the other, a Lorentz boost can be used to transform between the two frames. It involves performing transformations on both space and time coordinates.

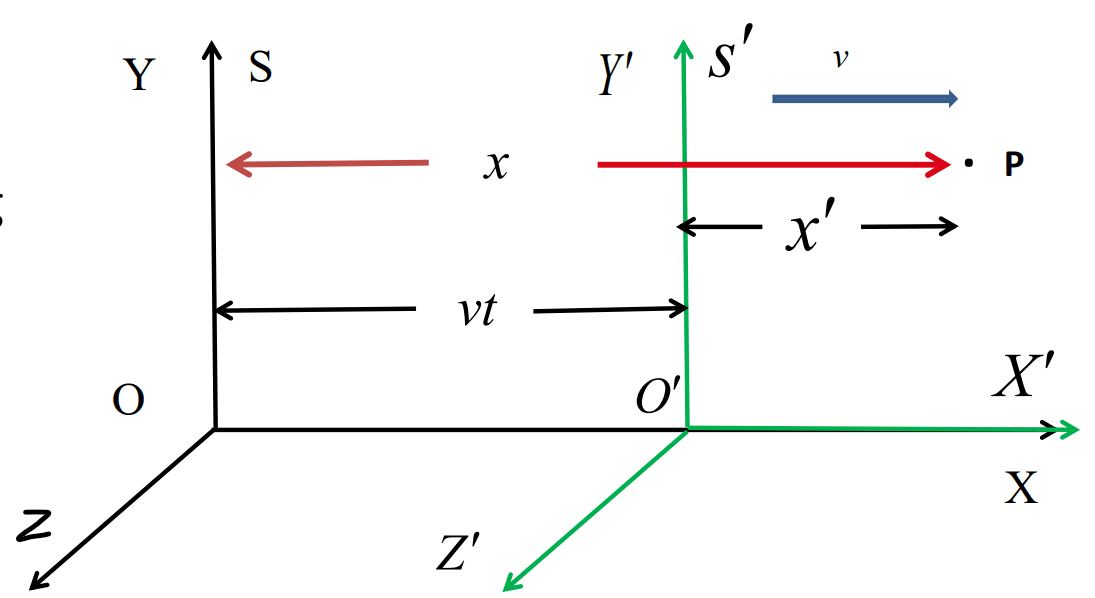
Let us consider two inertial frames $S$ and $S'$. $S$ is at rest and $S'$ is moving with a constant velocity $v$ relative to $S$ and along X-axis. Let an event is happening at point $P$ at a particular time.

Let the coordinates of $P$ with respect to $S$ is $(x ,y,z,t)$ and with respect to $S'$ is $(x',y',z',t')$. If $t = t'= 0$ , the origins of the both reference frames coincides with each other. $S'$ frame travelled a distance of $vt$ after $t$ seconds of time with respect to $S$ frame. $O$ and $O'$ are two observers.

According to Galilean Transformation eq.s :-

$x' = x - vt$

According to Lorentz Transformation eq., the measurement in X direction made in frame $S$ must be linearly proportional to that made in $S'$ frame. Hence a constant $K$ should be there So,

$x'= K(x - vt) \; \; \; \text{------ eq. 1}$

$x = K(x' + vt') \; \; \; \text{------ eq. 2}$

Using Einsteins $I^{st}$ postulate - All physics laws are valid & same for all inertial reference frame.

So put value of $x'$ in $\text{eq. 2}$

$x = K[K(x - vt) + vt']$

$\therefore \;\frac{x}{K}= Kx -Kvt + vt'$

$\therefore \;vt' = \frac{x}{K}-Kx+Kvt$

$\therefore \;t' = \frac{x}{Kv}-\frac{Kx}{v}+Kt$

$\therefore \; t' = Kt - \frac{Kx}{v} \left(1 - \frac{1}{K^2}\right) \; \; \; \text{------ eq. 3}$

Now, using Einsteins $II^{nd}$ postulate - Constancy of speed of light

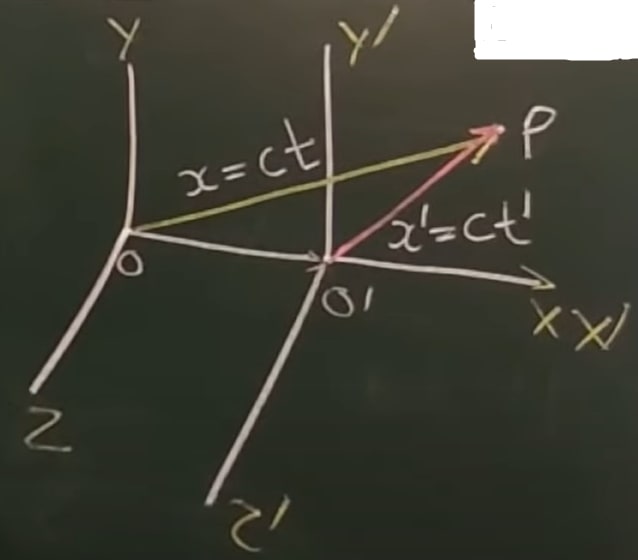
When two light beams flashes According to fig:-

$x = ct$ $\; , \;$ $x' = ct'$

Put these values in $eq. - 1$ and $eq. - 2$

From eq. 1 and 2,

$ct'= K(ct - vt) \; \; \text{------ eq. 4}$

$ct = K(ct' + vt') \; \; \text{------ eq. 5}$

To find value of constant K multiply eq 4 and 5

$c^2tt' = K^2 t(c-v)t(c+v)$

$K^2 = \frac{c^2}{c^2 - v^2} = \frac{c^2}{c^2 \left(1 - \frac{v^2}{c^2}\right)}$

$K = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}} \; \; \text{------ eq. 6}$

$1/K^2 = 1 - \frac{v^2}{c^2} \; \; \text{------ eq. 7}$

Put values from eq 6 and 7 into eq 1 and 3 :-

From eq. 1,

$x' = \frac{x-vt}{\sqrt{1 - \frac{v^2}{c^2}}} \; \; \text{------ eq. 8}$

From eq. 3,

$t' = K \left[ t - \frac{x}{v} \left(1 - \frac{1}{K^2}\right) \right]$

$t' = K \left[ t - \frac{x}{v} \left(1 - 1 + \frac{v^2}{c^2}\right) \right]$

$t' = \frac{t - \frac{xv}{c^2}}{\sqrt{1 - \frac{v^2}{c^2}}} \; \; \text{------ eq. 9}$

As there is not motion along Y and Z axes. Hence,

$y' = y \; \; \text{------ eq. 10}$

$z' = z \; \; \text{------ eq. 11}$

Hence, eq.s 8,9,10 and 11 are called Lorentz Transformation eq.s.

Numericals on Lorentz Transformations

Inverse Lorentz Transformation eq.s

From Lorentz Transformation eq.s :-

$x' = \frac{x-vt}{\sqrt{1 - \frac{v^2}{c^2}}}$

$t' = \frac{t - \frac{xv}{c^2}}{\sqrt{1 - \frac{v^2}{c^2}}}$

$y' = y$

$z' = z$

Now Inverse LT. eq.s can be written as :-

$x = \frac{x'+vt'}{\sqrt{1 - \frac{v^2}{c^2}}}$

$t = \frac{t' + \frac{x'v}{c^2}}{\sqrt{1 - \frac{v^2}{c^2}}}$

$y = y'$

$z = z'$