Relativistic Kinematics

Relativistic kinematics refers to the study of motion and interactions of objects that are moving at speeds comparable to the speed of light, as described by Albert Einstein's theory of special relativity. classNameical or Newtonian mechanics is a special case of kinematics that works well for objects moving at speeds much less than the speed of light. However, as an object's speed approaches the speed of light (denoted by c), classNameical mechanics fails to accurately describe its behavior.

Relativistic kinematics introduces corrections to classNameical kinematics when dealing with high speeds. Some key features of relativistic kinematics include:

1. Time Dilation: Time is relative, and it passes at different rates for observers in different reference frames. As an object approaches the speed of light, time for that object appears to pass more slowly for an observer at rest.

2. Length Contraction: Lengths of objects in motion appear shorter in the direction of motion as observed by an observer at rest.

3. Relativistic Momentum and Energy: classNameical concepts of momentum and kinetic energy are modified to incorporate relativistic effects. The total energy of an object includes not just its rest mass energy but also its kinetic energy due to motion.

4. Invariant Mass: While the relativistic mass of an object increases with its speed, the rest mass (or invariant mass) remains constant. The invariant mass is a fundamental property of the object and is the same in all reference frames.

5. Lorentz Transformations: These are mathematical equations that describe how space and time coordinates transform between different inertial frames in special relativity.

Velocity Addition Theorem

Derivation

Let us consider two frames $S$ and $S'$, frame $S'$ is moving with constant velocity $v$ relative to frame $S$ along the positive direction of the X-axis.

Let us express the velocity of the body in these frames. Suppose that body moves a distance $dx$ in time $dt$ in frame $S$ and through a distance $dx'$ in the time $dt'$ in the system $S'$ from point $P$ to $Q$. Then

$\frac{dx}{dt} = u\qquad \frac{dx'}{dt'}= u' \; \; \text{------ equation 1}$

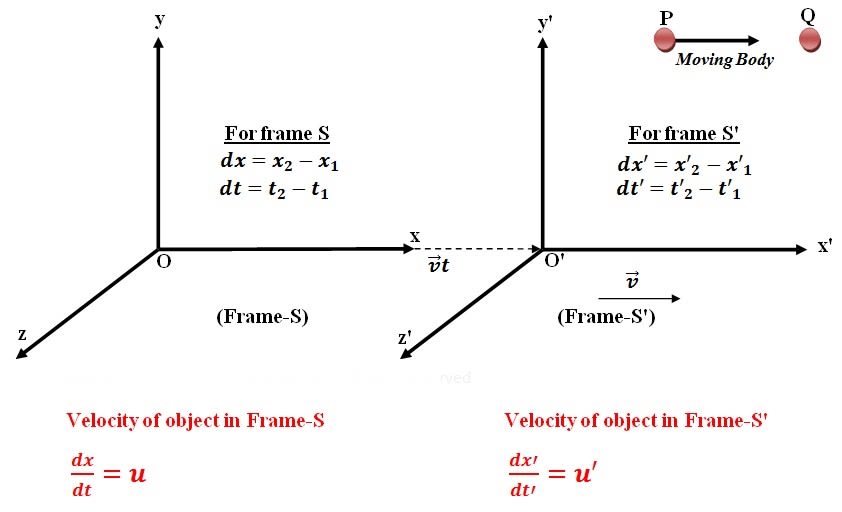
From Lorentz's inverse transformation

$x=K\left ( x'+vt' \right )\; \; \text{------ equation 2}$

$t=K '\left ( t'+\frac{v\cdot x'}{c^{2}} \right )\; \; \text{------ equation 3}$

Differentiate the $equation - 2$ and $equation - 3$ with respect to $t'$

$\frac{dx}{dt'}= K \left ( \frac{dx'}{dt'}+v \right )\; \; \text{------ equation 4}$

$\frac{dt}{dt'}= K ' \left ({1}+\frac{v}{c^{2}} \cdot \frac{dx'}{dt'} \right )\; \; \text{------ equation 5}$

Now divide the $equation - 4$ by $equation - 5$. So

$\frac{\frac{dx}{dt'}}{\frac{dt}{dt'}} = \left ( \frac{\frac{dx'}{dt}+v}{1+\frac{v}{c^{2}}\cdot \frac{dx'}{dt'} } \right ) \qquad$

From Lorentz Transformation $K =K '$. So above equation can be written as:

$\frac{dx}{dt} = \frac{u' +v}{1+ \frac{u'v}{c^{2}}}$

From $equation - 1$. The above equation can be written as:

$u = \frac{u' +v}{1+ \frac{u'v}{c^{2}}}$

This equation represents the relativistic law of addition of velocities with respect to an observer at frame-$S$ whereas in classNameical mechanics it is simply $u = u'+v$. There is the following point observed from the addition of the velocities equation.

• When $u' = c$, Then $u =\frac{c+v}{1+\frac{v}{c}}$ So, on solving we get

  $u=c$

• When $v = c$, Then $u =\frac{u'+c}{1+\frac{u'c}{c^{2}}}$ So, on solving we get

  $u=c$

• When $u' = c$ and $v = c$, Then $u =\frac{c+c}{1+\frac{c^2}{c^{2}}}$ So, on solving we get

  $u=c$

  This shows that the addition of the velocity of light simply reproduces the velocity of light. It means that the velocity of light in a vacuum is the maximum achievable velocity in nature and no signal and any object can travel faster than the velocity of light in a vacuum.

Numericals

Variation of Mass with Velocity

Derivation

Let there are two inertial frames of references $S$ and $S'$. $S$ is the stationary frame of reference and $S'$ is the moving frame of reference. At time $t=t'=0$ that is in the start, they are at the same position that is Observers $O$ and $O'$ coincides. After that $S$ frame starts moving with a uniform velocity $v$ along x axis.

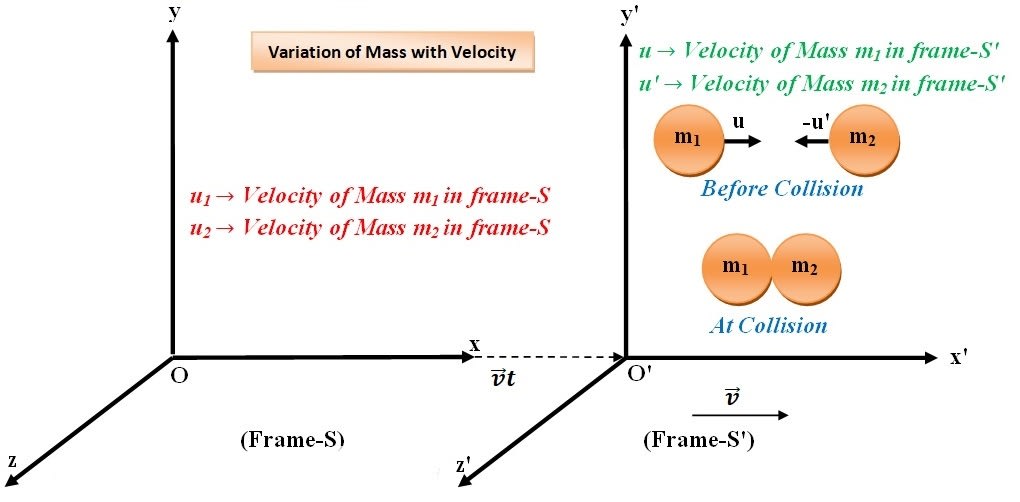
Suppose there are two particles moving in opposite direction in frame $S'$. Velocity of particle A will be $u$ and of B will be $-u'$ according to the observer $O'$.

Let us study the velocities and mass of these particles from frame $S$. Velocity of A is $u_1$ and B is $u_2$ from frame $S$ and these are given by velocity addition theorem:

$u_1 = \frac{u' + v}{1 + \frac{u'v}{c^2}}$ $\; \; and \; \;$ $u_2 = \frac{-u' + v}{1 - \frac{u'v}{c^2}}$ $\; \; \text{------ equation 1 and 2}$

Let $m_1$ and $m_2$ are the mass of A and B from frame $S$ respectively. As the particles are moving to each other, at certain instant they will collide and momentarily came to rest. But even when they came to rest, they travel with the velocity of the frame $S'$ that is with $v$.

According to the law of conservation of momentum:

Momentum before collision = Momentum after collision

Thus, $m_1u_1 + m_2u_2 = m_1v + m_2v = (m_1 + m_2)v \; \;$

$\text{------ equation 3}$

From $equation - 1\; and\; 2$, putting values of $u_1$ and $u_2$ in $equation - 3$, We get:-

$m_1 \frac{u' + v}{\left(1 + \frac{u'v}{c^2}\right)} + m_2 \frac{-u' + v}{\left(1 - \frac{u'v}{c^2}\right)} = (m_1 + m_2)v$

$m_1\left[\frac{u' + v}{1 + \frac{u'v}{c^2}} - v\right] = m_2\left[v - \frac{-u' + v}{1 - \frac{u'v}{c^2}}\right]$

Then take LCM of terms in the bracket and solve, we get

$m_1\left(\frac{1}{1 + \frac{u'v}{c^2}}\right) = m_2\left(\frac{1}{1 - \frac{u'v}{c^2}}\right)$

$or$

$\frac{m_1}{m_2} = \frac{1 + \frac{u'v}{c^2}}{1 - \frac{u'v}{c^2}}\; \; \text{------ equation 4}$

Now square $equation - 1$, then divide both sides by $c^2$ and subtract both sides by 1, we get

$1 - \frac{u_1^2}{c^2} = 1 - \frac{1}{c^2}\left(\frac{u' + v}{(1 + \frac{u'v}{c^2})}\right)^2$

By taking LCM on RHS and solving, we get

$1 - \frac{u_1^2}{c^2} = \frac{1 + \frac{u'^2v^2}{c^4} - \frac{u'^2}{c^2} - \frac{v^2}{c^2}}{(1 + \frac{u'v}{c^2})^2} \; \; \text{------ equation 5}$

Similarly by squaring $equation - 2$, then dividing both sides by $c^2$ and subtracting both sides by 1, we get

$1 - \frac{u_2^2}{c^2} = \frac{1 + \frac{u'^2v^2}{c^4} - \frac{u'^2}{c^2} - \frac{v^2}{c^2}}{(1 - \frac{u'v}{c^2})^2}\; \; \text{------ equation 6}$

On dividing $equation - 6\; \; by\; \; 5$, we get

$\frac{(1 - \frac{u_2^2}{c^2})}{(1 - \frac{u_1^2}{c^2})} = \frac{(1 + \frac{u'v}{c^2})^2}{(1 - \frac{u'v}{c^2})^2}$

Take square root on both sides

$\frac{\sqrt{1 - \frac{u_2^2}{c^2}}}{\sqrt{1 - \frac{u_1^2}{c^2}}} = \frac{1 + \frac{u'v}{c^2}}{1 - \frac{u'v}{c^2}} \; \; \text{------ equation 7}$

Now compare $equations - 4\; \; and\; \; 7$, we get

$\frac{m_1}{m_2} = \frac{\sqrt{1 - \frac{u_2^2}{c^2}}}{\sqrt{1 - \frac{u_1^2}{c^2}}}\; \; \text{------ equation 8}$

This is more of a complicated result. To make this result simple, let us assume that the particle B is in the state of rest from frame $S$ that is it has zero velocity before collision

Thus, $u_2 = 0$ $\; \; and \; \;$ $m_2 = m_0$

Where $m_0$ is the rest mass of the particle, Therefore $equation - 7$ becomes

$\frac{m_1}{m_0} = \frac{1}{\sqrt{1 - \frac{u_1^2}{c^2}}}$

Also assume $u_1 = v \; \; and \; \; m_1 = m$, Therefore above equation becomes

$\frac{m}{m_0} = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}$

$or$

$m = \frac{m_0}{\sqrt{1 - \frac{v^2}{c^2}}}$

This equation represents the equation of the variation of mass with the velocity. It shows that if a particle or anything moves with a speed comparable to the speed of the light then its mass will appeared increased.

Mass-Energy Equivalence

In classNameical mechanics, the mass of a moving particle is independent of its velocity. Contrary to this aspect, by Einstein’s special theory of relativity, the mass of a moving body depends upon its velocity and is given by

$$m = \frac{m_0}{\sqrt{1-v^2/c^2}} \quad \text{(i)}$$

where $v$ is the velocity of the body, $m_0$ is its rest mass and $c$ is the velocity of light. The increase in energy of the particle by the applications of force may be defined in terms of work done which is the product of the force and the displacement. According to Newton’s second law of motion, the rate of change of momentum of the particle is equal to the force applied on it. Thus

$$F = \frac{d(mv)}{dt} \quad \text{(ii)}$$

If the particle is displaced a distance $dx$ by the application of force $F$, the work done $Fdx$ is stored as kinetic energy $E_K$ in the body. Then

$$dW = dE_K = Fdx \quad \text{(iii)}$$

By using Eqs. (ii) and (iii), we get

$$dE_K = \frac{d(mv)}{dt} dx$$

or

$$dE_K = \frac{dx}{dt} d(mv) \quad \text{(iv)}$$

or

$$dE_K = v [dm + m d\nu]$$ $$= v^2 dm + m v d\nu \quad \text{(v)}$$

But

$$m = \frac{m_0}{\sqrt{1 - \frac{v^2}{c^2}}}$$

or

$$m^2 = \frac{m_0^2 c^2}{c^2 - v^2}$$

or

$$m^2 c^2 - m^2 v^2 = m_0^2 c^2 \quad \text{(vi)}$$

By differentiating Eq. (vi), we have

$$2m dm c^2 - 2m dv v^2 - 2v dm v = 0$$

or

$$dm c^2 = v^2 dm + m v dv \quad \text{(vii)}$$

By using Eqs. (v) and (vii), we get

$$dE_K = dm c^2 \quad \text{(viii)}$$

Thus, from Eq. (viii) it is clear that the change in kinetic energy is directly proportional to the change in mass. If the body is at rest, its velocity will be zero and hence the change in kinetic energy will be zero. Therefore, its mass will be $m_0$. If the body moves with velocity $v$, then its mass becomes $m$ and its kinetic energy becomes $E_K$. Therefore, by integrating equation (viii), we get

$$\int_0^{E_K} dE_K = c^2 \int_{m_0}^m dm$$

or

$$E_K = c^2 [m - m_0] = mc^2 - m_0 c^2$$

or

$$E = mc^2 = E_K + m_0 c^2 \quad \text{(ix)}$$

From Eq. (ix), it is clear that $E = mc^2$ is the total energy. It is the sum of kinetic and rest mass energy. That is,

$$E = mc^2$$

This relation is called Einstein’s mass energy relation.

Evidence For $E = mc^2$

1. Nuclear Reactions: In nuclear fission and fusion reactions, the total mass of the products is slightly less than the total mass of the reactants. This "missing" mass has been converted into energy, which is released in the reaction. For example, in the fusion reactions that power the sun, hydrogen nuclei fuse to form helium, releasing energy in accordance with $E = mc^2$.

2. Particle-Antiparticle Annihilation: When a particle meets its antiparticle, they annihilate each other, converting their total mass into energy, typically in the form of photons. For instance, when an electron and a positron annihilate, they produce gamma rays with an energy equivalent to the combined mass of the electron and positron.

3. Energy Production in Nuclear Power Plants: Nuclear power plants harness the energy released from fission reactions of heavy nuclei like uranium-235. The mass defect (difference in mass before and after the reaction) is converted into energy, demonstrating the principle of $E = mc^2$.

4. Experimental Measurements: Precise measurements of the masses of nuclei before and after reactions, and the energy released, confirm the mass-energy equivalence. Experiments with particle accelerators also validate the relationship, as the energy of particles moving close to the speed of light agrees with predictions from $E = mc^2$.

Einstein Relation Between Energy And Momentum