Galilean Transformation Equations

Theory And Derivation Of G T.

Galilean transformations are used to transform the coordinates of a particle from one inertial frame to another. They relate the observations of position and time made by two of observers, located in two different inertial frames.

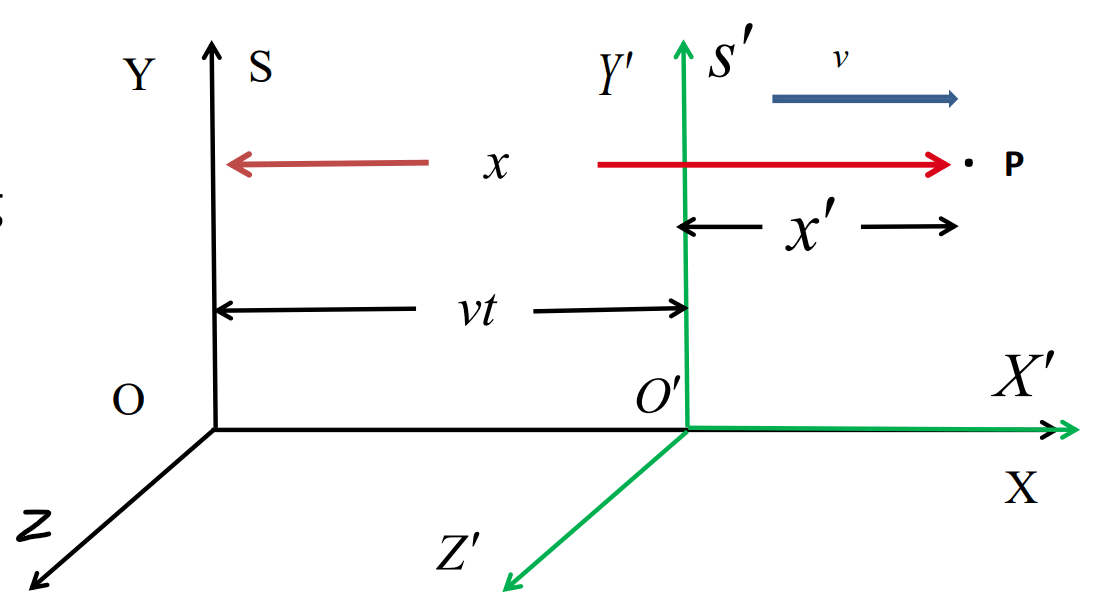
Let us consider two inertial frames $S$ and $S'$. $S$ is at rest and $S'$ is moving with a constant velocity $v$ relative to $S$. Let an event is happening at point $P$ at a particular time.

Let the coordinates of $P$ with respect to $S$ is $(x ,y,z,t)$ and with respect to $S'$ is $(x',y',z',t')$. If $t = t'= 0$ , the origins of the both reference frames coincides with each other. $S'$ frame travelled a distance of $vt$ after $t$ seconds of time with respect to $S$ frame. $O$ and $O'$ are two observers.

Let us choose our axes so that $X$ and $X'$ are parallel to v. Then the relation between these two frames can be written as

• $x' = x - vt$
• $y' = y$ (there is no relative motion along Y axes)
• $z' = z$ (there is no relative motion along Z axes)
• $t' = t$ (time is independent of space coordinate system)

The above equations are known as Galilean transformation Equations.

The inverse Galilean transformations can be expressed as under

• $x = x' + vt$
• $y = y'$ (there is no relative motion along Y axes)
• $z = z'$ (there is no relative motion along Z axes)
• $t = t'$

Veolcity And Acceleration Transformation Equations

Veolcity Transformation from G T. Equation - $x' = x - vt$. On differentiating w.r.t time :-

${u_x'= \frac{dx'}{dt}= \frac{d(x-vt)}{dt}=\frac{dx}{dt}-v}$

$u_x'= u_x - v$ in vector from $u' = u-v$

$u_y' = u_y \; , \; u_z' = u_z$

Acceleration Transformation - We know from Veolcity Transformation:-

$u_x'= u_x - v \; , \; u_y' = u_y \; , \; u_z' = u_z$

The acceleration components can be obtained by differentiating velocity equations with respect to time.

${a_x'= \frac{du_x'}{dt}= \frac{d(u_x-v)}{dt}=\frac{du_x}{dt}-\frac{dv}{dt}}$

$a_x' = a_x$ $\;(\therefore$ velocity v is constant$)$

$a_y' = a_y \; , \; a_z' = a_z$

$\therefore \; a' = a$

In vector form, ${a' = a}$ Multiplying this equation with mass on both sides, we get

$ma' = ma$

$F' = F$

The acceleration is same in both $S$ and $S'$ frames. So, acceleration and force are invariant in classNameical physics.

Numericals on Galilean Transformations

Drawbacks Of Galilean Transformation

1. The laws of electromagnetism or electrodynamics and Maxwell's equations are not invariant under Galilean transformations.

2. Galilean transformations are invalid when the objects are moving with nearer velocities of velocity of light.