Michelson And Morley Experiment

Theory Of Experiment

• The Michelson-Morley Experiment sought to detect the presence of luminiferous ether, a fictitious material which pervades space and is thought to carry light waves. The Michelson-Morley experiment was first performed in 1887 by Albert A. Michelson and Edward W. Morley to test the velocity of light. The objective of the Michelson-Morley experiment was to detect the relative motion of matter through all the stationary luminiferous ether. So, the setup employs the earth's motion all around the sun to create interference bands of light for the study. The experiment's goal was to see if light travels at the same velocity across all directions.
• It was thought to be proof of the hypothesis to say that the ether is dragged by or moves with a moving body. This result gave them more trust in order to detect the ether wind. A Michelson interferometer was used for the procedure. Albert Michelson invented an interferometer to measure the velocity of the Earth using ether and to measure the changing pattern of light.
• The experiment is known as “the most famous failed experiment” because, while the results were negative and they were unable to prove what they had hoped to prove, it allowed physicists to prove that the speed of light is constant in all circumstances, while also serving as a foundation for the theory of special relativity.

Derivation Of Experiment

A light beam from a monochromatic source S strikes a half-silvered glass plate P at a 45° angle to the beam. P divides the incident beam into two parts. The reflected portion travels perpendicular to the incident beam, falls normally at B on plane mirror M1, and is reflected back to P. It is refracted by P and then enters the telescope T.

The transmitted portion follows the initial beam's path, falls normally on mirror M2 at A, and is reflected back to P. It enters the telescope T after being reflected from the back surface of P. The upwardly reflected beam traverses the thickness of plate P three times, whereas the downwardly refracted beam traverses P only once. A compensating plate is used to make the effective distance of the mirrors M1 and M2 from plate P the same.

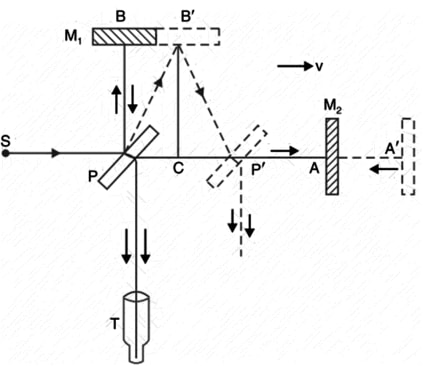
Assume that the apparatus's (or Earth's) velocity relative to fixed ether is v in the direction PA. The relative velocity of a light ray travelling along PA is (c - v), whereas the value for the returning ray is (c + v). Assume $PA=PB=d$

The time it takes light to travel from P to A is equal to ${ \frac{d}{c-v}}$.

The time it takes light to travel from A to P is equal to ${ \frac{d}{c+v}}$.

Total amount of time it takes light to travel from P to A and back

$t={ \frac{d}{c-v}} + { \frac{d}{c+v}} = { \frac{2cd}{c^2-v^2}} = { \frac{2d}{c} \left(1 + \frac{v^2}{c^2}\right)}$

Consider the upward-moving ray from P to B. Because of the earth's motion, it will strike the mirror M1 at $B'$ rather than B. If t 1 is the time it takes the ray to travel from P to M1, then $PB'=ct1$ and $BB'=vt1$.

The ray's total path until it returns to $P = PB'P'$.

Now, because $PB' = B'P', PB' + B'P' = 2PB'$

$(PB')^2 = PC^2 + (CB')^2 = (BB')^2 + PB^2$

$c^2t_1^2 = v^2t_1^2 + d^2$

$\therefore t_1 = { \frac{d}{\sqrt{c^2 - v^2}} \quad}$

Total time required for the ray to travel the entire path $PB' P'$

$t' = 2t_1 = { \frac{d}{\sqrt{c^2 - v^2}}} = { \frac{2d}{c \sqrt{1 - \frac{v^2}{c^2}}} = \frac{2d}{c}\left(1 + \frac{v^2}{2c^2}\right)}$

Obviously, $t' < t$. The difference in time is

$\triangle t = t - t'$

$= \frac{2d}{c}(1 + \frac{v^2}{c^2} - \frac{2d}{c})(1 + \frac{v^2}{2c^2})$

$= \frac{2d}{c} \times \frac{v^2}{2c^2}$

$= { \frac{dv^2}{c^3}}$

The time-travelled distance of light is $\triangle t = c \times \triangle t ={ \frac{dv^2}{c^2}}$

This is the difference in path between the two halves of the incident beam. The path difference between the two beams becomes ${ \frac{dv^2}{c^2}}$ when the apparatus is rotated 90°. When Michelson and Morley rotated their apparatus through 90°, they expected a fringe shift of about 0.4 and believed they could detect a shift as small as 0.01 of a fringe. However, no fringe displacement was observed during the experiment. They repeated the experiment at various points on the earth's surface and at different times of the year, and they found no measurable shift in fringes. This negative result implies that measuring the speed of the earth relative to the ether is impossible.

Negative Results Of Experiment

The theoretical Michelson Morley experiment results did not match the experimental results (Theoretically fringe shift result was not zero, it was about 0.4 but experimentally it was 0). Even back then, scientists believed that ether existed and that the earth moved in relation to it. As a result, there was a lot of debate and discussion about why there were negative results.

Then Einstein made his postulates, claiming that there is no such thing as ether.

Postulates Of Special Theory Of Relativity

Einstein provided two postulates for his theory of relativity:

• First Postulate: All physical laws are the same (or have the same form) in all inertial frames of reference moving with uniform velocities relative to each other. (This is also known as the law of equivalence.)
• Second Postulate: In free space or in vacuum, the speed of light is constant in all inertial frames of reference moving with uniform velocity in relation to each other. (This postulate is also known as the law of consistency or Constancy of speed of light.)