Oscillations

Periodic Motion : A motion that repeats itself in equal intervals of time is called periodic motion. It is also called harmonic motion.

Examples. 1. Revolution of earth round the sun or about its own axis, 2. Revolution of moon and other artificial satellites around the earth, 3. Rotation of the electrons round the nucleus of an atom, 4. The motion of pendulum of a clock, 5. Motion of prongs of a tuning fork and 6. Oscillations of a loaded spring.

The two common periodic motions are the simple harmonic motion and uniform circular motion.

Oscillatory Motion : The motion of a particle is oscillatory if it moves back and forth or to and fro about the same path at equal intervals of time.

Examples. 1. Motion of a pendulum, 2. Motion of mass attached to a suspended spring, 3. Motion of atoms in a molecule or a lattice, 4. Motion of particles of the medium through which sound travels, 5. Up and down motion of a floating object on water when waves propagate through it, 6. Motion of prongs of a tuning fork.

All oscillatory motions are periodic in nature but all periodic motions are not oscillatory. For example, revolution of earth round the sun is periodic but not oscillatory and Rotation of the electrons round the nucleus of an atom is periodic but not oscillatory.

Some Definitions:

1. The smallest time interval in which the motion repeats is called the Time Period (T). It is the time taken for one oscillation.
2. The number of repetitions of motion that occur per second is called the frequency (f) of the periodic motion. Frequency is equal to the reciprocal of time period. $f = \frac{1}{T}$.
3. The maximum displacement of a particle from its mean position during an oscillation is called amplitude (A) of oscillation.
4. Phase: It represents the state of motion of a particle in periodic motion. It is expressed in terms of fraction of period T or the fraction of angle $2\pi$ measured from the instant when the body has crossed the mean position in the positive direction.

Simple Harmonic Motion (SHM)

A particle is said to execute simple harmonic motion if the acceleration of the particle is directly proportional to the displacement of the particle from the mean position and it is directed towards the mean or equilibrium position. Ex. Oscillations of simple pendulum, oscillations of weight attached to spring.

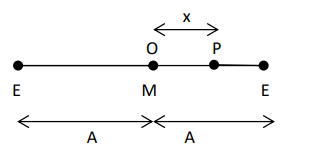
Consider a particle executing oscillatory motion about the mean position (E - M - E) with E as the extreme position and M is the mean position) with amplitude A. Let $x$ be the displacement of the particle at an instant of time t. A restoring force F acts on the particle to bring it back to its mean position. This force is directly proportional to the displacement.

Mathematically, $F ∝ x$

or

$F = -kx \; \; \; \text{---- equation 1}$

This equation is called as Hooke's law and represents the Restoring force. Where $k$ is spring constant and its value is depends on stiffness of the spring.

The negative sign indicates that F acts opposite to the direction of motion of the particle.

The acceleration of an object moving with simple harmonic motion can be found by using Hooke's law in the equation for Newton's second law.

$F=ma \; \; \; \text{---- equation 2}$

Comparing $\text{equation - 1}$ and $\text{equation - 2}$

$ma = -kx$

or

$a = -\left(\frac{k}{m}\right)x \; \; \; \text{---- equation 3}$

As $a= \frac{d^2x}{dt^2}$

$\text{equation - 3}$ becomes :-

$\frac{d^2x}{dt^2} = -\left(\frac{k}{m}\right)x$

or

$\frac{d^2x}{dt^2} + \left(\frac{k}{m}\right)x = 0 \; \; \; \text{---- equation 4}$

let $\frac{k}{m} = \omega^2$ where $\omega$ is called the angular velocity or angular frequency of oscillating particle.

Now, $\text{equation - 4}$ becomes :-

$\frac{d^2x}{dt^2} + w^2x = 0 \; \; \; \text{---- equation 5}$

$equation - 5$ is called differential equation of SHM.

Solution of Differential equation of SHM

Displacement of the particle

The differential form of SHM is $\frac{d^2x}{dt^2} + w^2x = 0$

or

$\frac{d^2x}{dt^2} = -w^2x$

Multiplying both the side of this equation by $2\frac{dx}{dt}$, we get

$2\frac{dx}{dt}\frac{d^2x}{dt^2} = -2\frac{dx}{dt}w^2x$

This equation can be expressed as:- $\frac{d}{dt}\left(\frac{dx}{dt}\right)^2 = -w^2\frac{d}{dt}\left(x\right)^2$

Integrating above equation we get:- $\left(\frac{dx}{dt}\right)^2 = -w^2x^2 + C\; \; \; \text{---- equation 1}$

Here, C is the constant of integration.

When the displacement is maximum, i.e. x = a, the velocity of the particle $\frac{dx}{dt}=v=0$

Putting this condition in equation 1 , $0 = -w^2a^2 + C$ $\; \; or \; \;$ $C=w^2a^2$

Now equation - 1 becomes, $\left(\frac{dx}{dt}\right)^2 = -w^2x^2 + w^2a^2$

or $\left(\frac{dx}{dt}\right)^2 = w^2\left(a^2 - x^2\right)$ $\; \; or \; \;$ $\frac{dx}{dt} = w\sqrt{\left(a^2 - x^2\right)}\; \; \; \text{---- equation 2}$

Equation - 2 is also the expression for the velocity of the particle executing SHM.

Rewriting equation - 2 as, $\frac{dx}{\sqrt{\left(a^2 - x^2\right)}} = wdt$

Integrating this equation, $\int\frac{dx}{\sqrt{\left(a^2 - x^2\right)}} = w\int dt$

gives,$\;$ $sin^{-1}\left(\frac{x}{a}\right) = wt + \varphi$

where $\varphi$ is the constant called the initial phase of the particle executing SHM. It is also called epoch.

or

$\left(\frac{x}{a}\right) = sin(\omega t + \varphi)$ $\; \; or \; \;$ $x = asin(\omega t + \varphi)$

The above equation is the solution of differential equation of SHM and is the expression for the displacement of the particle at time t.

Velocity of the particle executing SHM

If the initial position from where time is measured is the mean position, then $\varphi = 0$

Thus $x = asin(\omega t + \varphi)$ . The velocity of the particle at a given instant of time t is given by differentiating the above equation, i.e.

$\frac{dx}{dt} = a\omega \; cos\omega t$ $\; \; or \; \;$ $\frac{dx}{dt} = aw\sqrt{1 - sin^2 \omega t}$

As we know, $\; sin\omega t = \frac{x}{A}$, $\;$ we have, $\frac{dx}{dt} = a\omega\sqrt{1 - \frac{x^2}{a^2}}$ $\; \; or \; \;$ $\frac{dx}{dt} = a\omega\sqrt{\frac{a^2 - x^2}{a^2}}$

Thus the velocity of the particle is:- $\;$ $v = \frac{dx}{dt} = a\omega\sqrt{a^2 - x^2}$

Acceleration of the particle executing SHM

The displacement of the particle is given by $x = asin(\omega t + \varphi)$. If the particle starts from mean position when t = 0, then initial phase $\varphi = 0$ . Thus the above equation is

$x = asin\omega t$

On Differentiating we get,

$\frac{dx}{dt} = a\omega cos\omega t$

Differentiating again, we get $\;$ $\frac{d^2x}{dt^2} = -a\omega^2 sin\omega t = -a\omega^2\left(\frac{x}{a}\right)$

We know, $\; sin\omega t = \frac{x}{a}$

or the acceleration $\; \frac{d^2x}{dt^2} = a = -\omega^2 x$.

This gives the expression for the acceleration of the particle executing SHM.

Time period of a particle executing SHM

The angular frequency of the particle executing SHM is given by $\omega = 2\pi f$ where $f$ is the frequency. As $f=\frac{1}{T}$, where $T$ is the time period of SHM, we get $\omega = \frac{2\pi}{T}$ or ,

$T = \frac{2\pi}{\omega}$

This equation can be written as:- $T=2\pi \sqrt{\frac{1}{\omega^2}}\; \; \; \text{---- equation 1}$

We know, $w^2 = \frac{a}{x}$

So Equation - 1 becomes,

$T = 2\pi \sqrt{\frac{x}{a}}$

As $a = \left(\frac{k}{m}\right)x$, and $a = \omega^2x$

Also we have assumed above $\omega^2 = \frac{k}{m}$

leading to $T=2\pi \sqrt{\frac{m}{k}}$

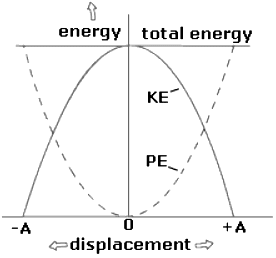
Energy of SHM

Consider a particle executing SHM represented by $y=asin(\omega t+\varphi)$. The velocity of the particle is $v=\omega\sqrt{A^2-\omega^2}$ and its acceleration is $a=-\omega^2x$.

The energy of the particle is the sum of its kinetic and potential energies. The particle having a displacement x is further moved through a small distance dx, then the work done:-

$dW = -F \times dx = -ma \times dx$

As $a = -\omega^2x$, the work done is $dW= -m(-\omega^2x) \times dx$

or

$dW = m\omega^2xdx$

Total work done in moving the particle from 0 to x is given by integrating the above equation,

$\int dW = \int_0^x m\omega^2xdx$

or

$E_p = W = \frac{1}{2}m\omega^2x^2$

This expression gives the potential energy $E_p$ of the particle.

The kinetic energy of the particle is $E_K = \frac{1}{2}mv^2$.

As $v=\omega\sqrt{A^2-x^2}$

Kinetic Energy becomes:- $E_K = \frac{1}{2}m \omega^2(A^2 - x^2)$

The total energy of the particle is $E=E_P + E_K$

$\therefore \; E = \frac{1}{2}m\omega^2x^2 + \frac{1}{2}m \omega^2(A^2 - x^2)$

So, $\: E = \frac{1}{2}m\omega^2A^2$ $\; \; or \; \;$ $\: E = \frac{1}{2}m(2\pi f)^2A^2$ $\; \; or \; \;$ $E=2\pi^2 m f^2 A^2$

Average Values of Kinetic and Potential energy of SHM

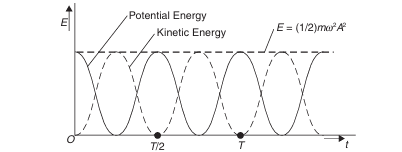
Suppose a particle of mass $m$ executes SHM of period $T$. The displacement of the particles at any instant t is given by, $x = Asin(\omega t + \theta)$ and velocity is given by, $v = \frac{dx}{dt} = \omega A cos(\omega t + \theta)$

Instantaneous Kinetic Energy $E_K$ is given by:-

$E_K = \frac{1}{2}mv^2 = \frac{1}{2}m\omega^2A^2cos^2 (\omega t + \theta)$

if $T$ is time period, then

Average K.E. = $\frac{1}{T}\int_0^T{\frac{1}{2}m\omega^2A^2cos^2 (\omega t + \theta)dt}$

$= \frac{mA^2\omega^2}{2T}\int_0^T{cos^2(\omega t + \theta)dt}$

$= \frac{mA^2\omega^2}{2T}\int_0^T\frac{1}{2}[1 + cos2(\omega t + \theta)]dt$

$= \frac{mA^2\omega^2}{4T}\left[\int_0^T{cos2(\omega t + \theta)dt}\right]$

$= \frac{mA^2\omega^2}{4T}T$

$= \frac{1}{4}mA^2\omega^2$

Instantaneous Potential Energy $E_P$ is given by:-

$E_P = \frac{1}{2}kx^2 = \frac{1}{2}kA^2sin^2 (\omega t + \theta)$

Average P.E. = $\frac{1}{T}\int_0^T{\frac{1}{2}kA^2sin^2(\omega t + \theta)dt}$

$=\frac{kA^2}{2T}\int_0^T{\frac{1}{2}[1 - cos2(\omega t + \theta)dt]}$

$=\frac{kA^2}{4T}\left[\int_0^T{dt} - \int_0^T{cos2(\omega t + \theta)dt}\right]$

$=\frac{kA^2}{4T}T = \frac{1}{4}kA^2$

We know, $k = m\omega^2$

$\therefore \;$ Average P.E. = $\frac{1}{4}mA^2\omega^2$

Thus, Total Energy = $E_K + E_P = \frac{1}{2}mA^2\omega^2$

Thus it is clear that the average kinetic energy of a SHM is equal to the average potential energy and is equal to half the total energy.

Total energy of the oscillating particle is the same at every point of oscillation

The expression for kinetic energy is $E_K = \frac{1}{2}m\omega^2(A^2 - x^2)\; \; \; \text{---- equation 1}$

and potential energy expression is $E_p = \frac{1}{2}m\omega^2x^2\; \; \; \text{---- equation 2}$

The total energy at any point of oscillation is

$E = E_P + E_K = \frac{1}{2}mw^2A^2\; \; \; \text{---- equation 3}$

• At the extreme position, $x=A$ and thus from $equation - 1$ kinetic energy is zero (as the velocity is also zero). Thus $E_K = 0$. Also from $equation - 2$ As $x=A$, at the extreme position, potential energy is $E_P = \frac{1}{2}m\omega^2A^2$

  Total energy $E = E_P + E_K = \frac{1}{2}m\omega^2A^2\; \; \text{---- equation 4}$

• At the mean position, kinetic energy is maximum as the velocity is maximum. Also as $x=0$ at mean position, from $equation - 1\;,$ $E_K = \frac{1}{2}mw^2A^2$

  and as $x=0$, at the mean position, from $equation-2\:,$ $E_P = 0$.

Thus total energy $E = E_P + E_K = \frac{1}{2}m\omega^2A^2\; \; \; \text{---- equation 5}$

Thus from $equations - 3,4\: and \:5$ it is clear that total energy remains same at every point of oscillation.

Numericals on SHM