Forced Oscillations

Forced oscillations occur when an external periodic force is applied to a system, causing it to oscillate at a frequency other than its natural frequency. This force can be applied in various forms, such as mechanical, electrical, or gravitational forces. Examples include pushing a swing or an electrical oscillator.

Forced oscillations are also known as forced vibrations. When the frequency of the external periodic force matches the natural frequency of the system, resonance occurs, leading to a significant increase in the amplitude of oscillation. This phenomenon is commonly referred to as frequency resonance.

In forced oscillations, the amplitude of oscillation may experience damping, which can decrease the amplitude over time. However, if the external energy supplied to the system matches or exceeds the energy loss due to damping, the amplitude can remain relatively constant.

When a forced oscillation system is subjected to a sudden change in the external force (such as its frequency or amplitude), the system needs some time to adjust to this change and reach a new steady-state behavior. During this adjustment period, the oscillations exhibit transient behavior, characterized by changes in amplitude, phase, and other oscillatory parameters.

The transient effects in forced oscillations typically decay over time as the system approaches its new steady-state behavior. The duration and magnitude of the transient effects depend on various factors such as the system's damping, the nature of the external force, and the initial conditions of the system.

Differential equation of FHO

Consider a body of mass $m$ oscillating under the action of an external periodic force $F_e = F_0sinpt$ where $F_0$ is the maximum value of this force and $p$ is angular frequency.

The body also experiences restoring force $F_r=-kx$ where $x$ is the displacement of body at an instant of time $t$ and frictional force $F_d = -rv$ where $r$ - damping constant and $v=\frac{dx}{dt}$ along with the periodic force.

Then, Total force acting on body is:-

$F = F_r + F_d + F_e$

From Newton's second law, $F = ma = m\frac{d^2x}{dt^2}$

Thus, above equation becomes:-

$m\frac{d^2x}{dt^2} = -kx + -r\frac{dx}{dt} + F_0sinpt$

On dividing above equation by $m$ we get,

$\frac{d^2x}{dt^2} + \frac{k}{m}x + \frac{r}{m}\frac{dx}{dt} = \frac{F_0}{m}sinpt$

On Putting, $\frac{k}{m} = \omega^2\;,\; \frac{r}{m} = 2b\;\:\text{and}\;\: \frac{F_0}{m}=f_0$ we get,

$\frac{d^2x}{dt^2} + 2b\frac{dx}{dt} + \omega^2x = f_0sinpt \; \; \; \text{----- equation 1}$

This is the differential equation for forced harmonic oscillator.

Solution of differential equation of FHO

The complete solution of above differential equation is given by the sum $(x)$ of complementary function $(x_1)$ and particular integral $(x_2)$

i.e. $x = x_1 + x_2 \; \; \text{----- equation - A}$

• To find complementary function $(x_1)$ [Transient State]. Put R.H.S of above differential equation to 0, we get:-

  $\frac{d^2x}{dt^2} + 2b\frac{dx}{dt} + \omega^2x = 0$

  This is the differential equation for damped harmonic oscillator whose solution in case of light damping $(b^2< \omega^2 )$ is given as:-

  $x_1 = ae^{-bt}[sin(nt + \Phi)]$ where, $n=\sqrt{\omega^2 - b^2}$ represents the frequency of oscillation, and $Φ_1$ is the phase angle and $a=\frac{x_0}{n}$.

  In above equation the amplitude $ae^{-bt}$ decays exponentially with time. The motion therefore after sufficiently long time dies down, so this state is called Transient State.

• To find Particular Integral $(x_2)$ [Steady State].

  When the external periodic force is applied on the oscillator, then the driving force tends to make the oscillator to oscillate with frequency of driving force but oscillator itself want to oscillate with its own natural frequency. But after sufficiently long time, transients die down (due to amplitude decaying exponentially with time) and ultimately the oscillator performs oscillations at frequency of driving force. This is called Steady State.

  Let $x_2 = Asin(pt-\Phi)\; \; \text{----- equation 2}$ be particular integral of equation 1.

  On differentiating above equation twice, we get:-

  $\frac{dx}{dt} = Apcos(pt-\Phi)$

  $\frac{d^2x}{dt^2} = -Ap^2sin(pt-\Phi)$

  Putting these values in equation 1, we get:-

  $-Ap^2sin(pt-\Phi) + 2b[Apcos(pt-\Phi)] +$

  $\omega^2Asin(pt-\Phi) = f_0sinpt$

  $Asin(pt-\Phi)[\omega^2 - p^2] +$

  $2b[Apcos(pt-\Phi)] = f_0sin((pt-\Phi) + \Phi)$

  We know, $sin(A+B) = sinAcosB + cosAsinB$

  $Asin(pt-\Phi)[\omega^2 - p^2] +$

  $2b[Apcos(pt-\Phi)] =$

  $f_0[sin(pt-\Phi)cos\Phi + cos(pt-\Phi)sin\Phi]$

  $Asin(pt-\Phi)[\omega^2 - p^2] +$

  $2b[Apcos(pt-\Phi)] =$

  $f_0sin(pt-\Phi)cos\Phi + f_0cos(pt-\Phi)sin\Phi$

  On Equating the coefficient of $sin(pt-\Phi)$ and $cos(pt-\Phi)$ we get,

  $A[\omega^2 - p^2] = f_0cos\theta \; \; \text{----- equation 3}$

  $2bAp = f_0sin\Phi \; \; \text{----- equation 4}$

  On squaring and adding above two equations we get,

  $A^2[\omega^2 - p^2]^2 + 4b^2A^2p^2 = f_0^2$

  or

  $A = \frac{f_0}{\sqrt{(\omega^2 - p^2)^2 + 4b^2p^2}}$

  This is the expression for amplitude of forced oscillation.

  Now, to find phase of forced oscillations, divide equation 4 by 3 we get,

  $tan\phi = \frac{2bp}{\omega^2 - p^2}$

  The phase difference $\Phi = tan^{-1}\frac{2bp}{\omega^2 - p^2}$

  Putting values of $A$ and $\Phi$ in equation - 2 we get,

  $x_2 = \frac{f_0}{\sqrt{(\omega^2 - p^2)^2 + 4b^2p^2}}sin(pt - tan^{-1}\frac{2bp}{\omega^2 - p^2})$

Now putting values of $x_1$ and $x_2$ in equation - A we get,

$x = ae^{-bt}[sin(nt + \Phi)] +$

$\frac{f_0}{\sqrt{(\omega^2 - p^2)^2 + 4b^2p^2}}sin(pt - tan^{-1}\frac{2bp}{\omega^2 - p^2})$

First term represents the natural damped oscillation and the second term represents the forced oscillation. Initially both the vibrations will be present, but with the passage of time, the first term vanishes and the motion of the body will be completely represented by the second term.

So the solution is only,

$x = \frac{f_0}{\sqrt{(\omega^2 - p^2)^2 + 4b^2p^2}}sin(pt - tan^{-1}\frac{2bp}{\omega^2 - p^2})$

Case I: Low driving frequency

When $(p < \omega)$, we have, $A = \frac{f_0}{\sqrt{(\omega^2 - p^2)^2 + 4b^2p^2}}$

On neglecting $p^2$, then $A = \frac{f_0}{\omega^2} = \frac{F_0/m}{\omega^2}$ or $A = \frac{F_0}{m\omega^2}$

Here, amplitude depends on force constant and mass.

For $(p < \omega)$, $\Phi = tan^{-1}(0) = 0$

The force and displacement are always in phase.

Case II: High driving frequency

When $(p > \omega)$, we have, $A = \frac{f_0}{\sqrt{(\omega^2 - p^2)^2 + 4b^2p^2}}$

On neglecting $\omega^2$, then $A = \frac{f_0}{\sqrt{p^4 + 4b^2p^2}}$

Here, amplitude varies inversely with damping constant b and applied frequency p.

For $(p > \omega)$, $\Phi = tan^{-1}(\frac{-2bp}{p^2}) =\frac{-2b}{p}$

if b is small, then $\frac{2b}{p} = 0$, so $\Phi = tan^{-1}(0) = π$

The displacement lags behind the force by a phase by π which means they are out of phase.

Case III : Resonance

Resonance is the condition where the applied frequency matches with the natural frequency.

There are two conditions for resonance:

• The applied frequency $p$ should be equal to natural frequency $\omega$ of a body.
• The damping constant $b$ should be minimum.

When $(p = \omega)$, we have, $A = \frac{f_0}{\sqrt{(\omega^2 - p^2)^2 + 4b^2p^2}}$

On putting $\omega = p$, then $A_{max} = \frac{f_0}{\sqrt{4b^2p^2}} = \frac{F_0/m}{\sqrt{4b^2p^2}}$ or $A = \frac{F_0}{2mb\omega}$

Here, amplitude varies inversely with damping force b. As damping force decreases, the amplitude of vibrating body increases. This leads to Resonance.

At resonance, the amplitude of oscillations is maximum. For small values of $b$ (low damping ), the amplitude decreases very rapidly on either side of the resonant frequency than for higher value of $b$.

Also we know, $\tau = \frac{1}{2b}$

$\therefore \; A_{max} = \frac{f_0 \tau}{\omega}$ , where $\tau$ is relaxation time.

For $(p = \omega)$, $\Phi = tan^{-1}(\frac{-2b\omega}{0}) = tan^{-1}(\infty) = \frac{π}{2}$

The displacement lags behind the force by a phase by $\frac{π}{2}$.

Examples:-

1. Swinging on a swing: Pushing a swing at its natural frequency amplifies its motion, demonstrating mechanical resonance.
2. LC circuit: Resonance occurs in electrical circuits containing inductance and capacitance when the frequency of the applied alternating current matches the circuit's natural frequency.
3. Guitar strings: Strings on musical instruments resonate when plucked or bowed at their natural frequencies, producing sound.
4. Structural resonance in buildings: Vibrations from machinery or external forces can resonate with a building's natural frequency, leading to structural damage or collapse.
5. Nuclear Magnetic Resonance (NMR): Nuclei in a magnetic field absorb and reemit electromagnetic radiation at their resonant frequencies, used in MRI machines and spectroscopy.

Sharpness of Resonance

The term sharpness of resonance refers to the rate of fall in amplitude with the change of driving frequency on either side of resonant frequency. Resonance is said to be sharp, when for a small change of the driving frequency from the resonant frequency, there is a large change in the energy of vibration.

When the damping is low, the amplitude falls of a very rapidly on either side of resonant frequency
and that the resonance is sharp. Example for sharp resonance is a sonometer wire with a tuning fork.

When the damping is high, the amplitude falls of very slowly on either side of resonant frequency and that the resonance is flat. Example for flat resonance is resonance of an air column.

When damping is zero, When damping is zero, theoretically, the amplitude of the system's oscillation would become infinite at the resonant frequency. However, in reality, there is always some form of damping present in physical systems, even if it is very small. This means that the amplitude cannot truly become infinite, although it may become extremely large if damping is negligibly small.

The figure shows the variation of amplitude with driving frequency.

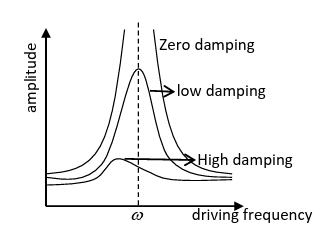
Sharpness of resonance is defined by the Q factor. Q measures sharpness of resonance. Quality factor at resonance is defined as the ratio of amplitude at resonance to the amplitude at zero driving frequency.

$Q = \frac{A_{max}}{A_{p=0}} = \frac{f_0/2b\omega}{f_0/\omega^2} = \omega \tau$, where $\tau$ is $\frac{1}{2b}$ and is relaxation time.