Damped Oscillations

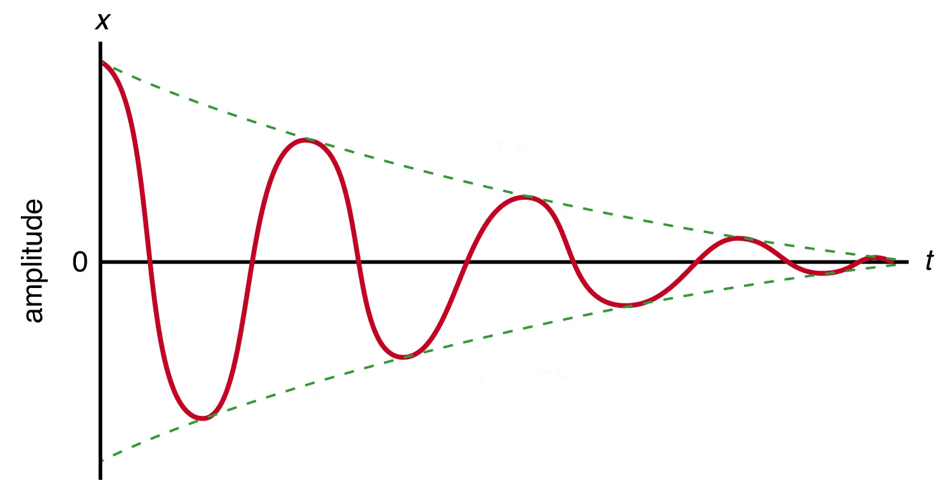
In real oscillating systems, mechanical energy is lost from the system due to frictional or any other dissipative forces leading to decrease in amplitude and finally oscillations stop.

If the amplitude of the oscillations of a system decreases with time then it is called damped oscillations. If the oscillations of a system persist without any change in its amplitude then it is called undamped oscillations.

Damped harmonic motion is defined as decay or decrease of amplitude of motion with respect to time in presence of air or other medium. The oscillator which performs such type of motion is known damped harmonic oscillator.

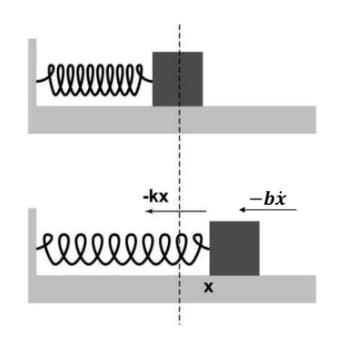
Consider a body executing damped harmonic oscillations. Let x be the displacement of the body from its mean position at an instant of time t.

Let $v=\frac{dy}{dt}$ be its instantaneous velocity.

The vibrating body is constantly acted upon by restoring force given by,

$F_{restoring} = -kx$

where k - force constant and x - displacement

The damping force always acts in a opposite directions to that of motion of oscillatory body and velocity dependent.

$F_{damping} \propto -v$

$F_{damping} \propto -rv$

where r - damping constant

The total force acting on the body is:- $F_{net}= F_{restoring}+F_{damping}$

$F_{net}= -kx + -rv \; \; \; \text{----- equation 1}$

$F_{net}= -kx + -r\frac{dx}{dt}$

From Newton's second law, $F_{net} = ma = m\frac{d^2x}{dt^2}$

equation - 1 becomes:- $\; m\frac{d^2x}{dt^2} = -kx -r\frac{dx}{dt}$

or

$m\frac{d^2x}{dt^2} + kx + r\frac{dx}{dt} = 0$

or

$\frac{d^2x}{dt^2} + \frac{k}{m}x + \frac{r}{m}\frac{dx}{dt} = 0 \; \; \; \text{----- equation 2}$

let $\frac{r}{m} = 2b \; \;and\; \; \frac{k}{m} = \omega^2$

where $\omega$ is natural frequency of oscillating body.

Hence, equation - 2 becomes:- $\; \frac{d^2x}{dt^2} + \omega^2x + 2b \frac{dx}{dt} = 0 \; \; \; \text{----- equation 3}$

The general solution of above equation is given by:- $\; x = Ae^{\alpha t} \; \; \; \text{----- equation A}$

On differentiating above equation twice we get,

$\frac{dx}{dt} = A\alpha e^{\alpha t}$

$\frac{d^2x}{dt^2} = A\alpha^2 e^{\alpha t}$

Putting values of $\frac{dx}{dt}$ and $\frac{d^2x}{dt^2}$ and x in equation - 3

$A\alpha^2 e^{\alpha t} + \omega^2 Ae^{\alpha t} + 2b A\alpha e^{\alpha t} = 0$

$Ae^{\alpha t}(\alpha^2 + 2b\alpha + \omega^2) = 0$

As, $Ae^{\alpha t} ≠ 0$

$\therefore \; (\alpha^2 + 2b\alpha + \omega^2) = 0$

Using quadratic formula,

$\alpha = \frac{{-2b \pm \sqrt{{4b^2 - 4\omega^2}}}}{{2}}$

$\therefore \; \alpha = -b \pm \sqrt{b^2 - \omega^2}$

$\therefore \; \alpha_1 = -b + \sqrt{b^2 - \omega^2}$

$\therefore \; \alpha_2 = -b - \sqrt{b^2 - \omega^2}$

So, $\; x = Ae^{\alpha_1 t} + Be^{\alpha_2 t}$

Hence, the general solution of equation - 3 is given by,

$x = Ae^{(-b + \sqrt{b^2 - \omega^2})} + Be^{(-b - \sqrt{b^2 - \omega^2})}$

where A and B are constants.

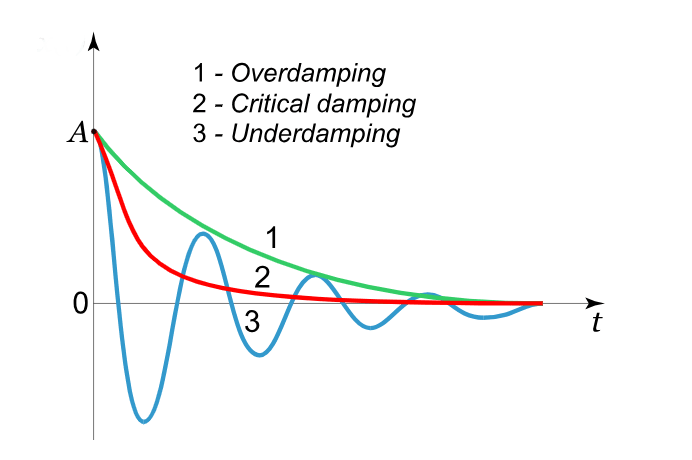
Different Damping Conditions

• Case 1: Over damping

  For Over damping, $b^2> \omega^2 \;$ indicating a high level of damping. Consequently, $\sqrt{b^2-\omega^2}$ is positive. Under this condition, the system returns to its equilibrium position slowly without oscillating. Overdamped systems exhibit no oscillations, but the return to equilibrium can be slow due to high friction or damping. Such a motion is called dead-beat or aperiodic.

• Case 2: Critical damping

  For Critical damping, $b^2 = \omega^2 \;$ , signifying a damping level that just prevents oscillation. The solution to the differential equation takes the form $x = e^{-bt}(P+Qt)$, where $P$ and $Q$ are constants determined by initial conditions. Critical damping ensures the system returns to its mean position without oscillating and achieves this return as quickly as possible without overshooting or exceeding the equilibrium position.

• Case 3: Under damping

  For Under damping, $b^2< \omega^2 \;$ , indicating less damping compared to the critical damping case. In this situation, $\sqrt{b^2 - \omega^2}$ is an imaginary number with a negative real part. The solution to the differential equation takes the form $x = ae^{-bt}[sin(nt + \Phi)]$ where $n=\sqrt{\omega^2 - b^2}$ represents the frequency of oscillation, $x_0$ is the initial displacement, and $Φ$ is the phase angle and $a=\frac{x_0}{n}$. Underdamped systems continue to oscillate with decreasing amplitude until eventually returning to their initial state. This motion is oscillatory.

Power Dissipation

Whenever the system is set into oscillations, its motion is opposed by frictional (damping) forces due to air resistance. The work done against these forces is dissipated out in the form of heat. So the mechanical energy of the system continuously decreases with time and amplitude of oscillation gradually decays to zero.

We consider the time average condition we assume that the amplitude remains nearly constant in one oscillation

We know,

Average K.E. of harmonic oscillator in ideal case = $\frac{1}{4}mA^2\omega^2$

However in practical case (damped oscillation) , Average K.E. is = $\frac{1}{4}mA^2\omega^2e^{-2bt} \; \; \; \text{----- equation 1}$

Similarly, Average P.E. of harmonic oscillator in ideal case = $\frac{1}{4}mA^2\omega^2$

and in practical case (damped oscillation) = $\frac{1}{4}mA^2\omega^2e^{-2bt} \; \; \; \text{----- equation 2}$

On adding equation 1 and 2 we get,

Total Energy $E$ = $\frac{1}{4}mA^2\omega^2e^{-2bt} + \frac{1}{4}mA^2\omega^2e^{-2bt}$

$= \frac{1}{2}mA^2\omega^2e^{-2bt} \; \; \; \text{----- equation 3}$

We know $E_0 = \frac{1}{2}mA^2\omega^2$

$\therefore \;$ equation - 3 becomes,

$E = E_0e^{-2bt}$

Since, The Rate of dissipation of energy is called power dissipation i.e. = $P = -\frac{dE}{dt}$

$\therefore \; P = -\frac{d}{dt}E_0e^{-2bt} = E_0e^{-2bt}2k$

We know, $k = \frac{1}{2\tau}\; \;$, Here $\tau$ is relaxation time and $E = E_0e^{-2bt}$

Above equation becomes,

$P =E_0e^{-2bt}2\frac{1}{2\tau} =\frac{E}{\tau}$

Quality Factor

The quality factor is defined as $2$ times the ratio of the energy stored in the system to the energy lost per period.

$Q = 2\pi \frac{\text{energy stored in system}}{\text{energy lost per period}} = 2\pi \frac{E}{PT}$

where $P$ is power dissipated and $T$ is periodic time. We know that $P = \frac{E}{\tau},\;$ where $\tau$ is relaxation time. So,

$Q=2\pi \frac{E}{\frac{E}{\tau}T} = \frac{2\pi \tau}{T} = \omega \tau$

where $\omega = \frac{2\pi}{T} = \text{angular frequency}$

Higher the value of $Q$, higher would be the value of relaxation time $\tau$. (i.e. as $Q$ is high, damping is low.)

Relaxation Time

Relaxation time $(\tau)$ is the time after which the energy reduces to $(\frac{1}{e})^{th}$ of its initial value $E_0$. If $\tau$ is the relaxation time, then at $t = \tau$ , $E = \frac{E_0}{\tau}$

We know, $E = E_0e^{-2bt}$

On Comparing, $\frac{E_0}{\tau} = E_0e^{-2bt}$

we get relaxation time $\tau$ = $\frac{1}{2b}\:,\;$ where $b$ is damping coefficient.

So, energy can be expressed as $E = E_0e^{-\frac{t}{\tau}}$