Star-Delta Transformation

The star-delta transformation, also known as the delta-star transformation, is a technique used in electrical circuit analysis to simplify complex networks, particularly those involving resistors or impedances. This transformation involves converting either a star $(Y)$ configuration to a delta $(\triangle)$ configuration or vice versa.

Delta To Star Conversion

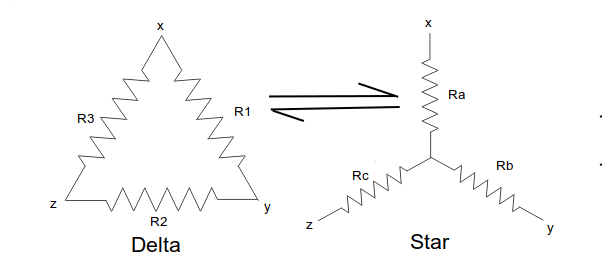
Consider a delta system that has three corner points that are $x$, $y$ and $z$ as shown in the figure. Electrical resistance of the branch between points $x$ and $y$, $y$ and $z$ and $z$ and $x$ are $R_1$, $R_2$ and $R_3$ respectively.

The resistance between the points $x$ and $y$ will be,

$R_{xy} = R_1 || (R_2 + R_3) = \frac{R_1.(R_2 + R_3)}{R_1 + R_2 + R_3}$

Now, one star system is connected to these points $x$, $y$, and $c$ as shown in the figure. Three arms $R_a$, $R_b$ and $R_c$ of the star system are connected with $x$, $y$ and $z$ respectively. Now if we measure the resistance value between points $x$ and $y$, we will get,

$R_{ab} = R_a + R_b$

Since the two systems are identical, resistance measured between terminals $x$ and $y$ in both systems must be equal.

$R_a + R_b = \frac{R_1.(R_2+R_3)}{R_1 + R_2 + R_3} \; \; \text{-------- equation 1}$

Similarly, resistance between points $y$ and $z$ being equal in the two systems,

$R_b + R_c = \frac{R_2.(R_3+R_1)}{R_1 + R_2 + R_3} \; \; \text{-------- equation 2}$

And resistance between points $z$ and $x$ being equal in the two systems,

$R_c + R_a = \frac{R_3.(R_1+R_2)}{R_1 + R_2 + R_3} \; \; \text{-------- equation 3}$

Adding equations (1), (2) and (3) we get,

$2(R_a + R_b + R_c) = \frac{2(R_1.R_2 + R_2.R_3 + R_3.R_1)}{R_1 + R_2 + R_3}$

$R_a + R_b + R_c = \frac{R_1.R_2 + R_2.R_3 + R_3.R_1}{R_1 + R_2 + R_3} \; \text{--- equation 4}$

Subtracting equations (1), (2) and (3) from equation (4) we get,

$R_a = \frac{R_3.R_1}{R_1 + R_2 + R_3} \; \; \text{-------- equation 5}$

$R_b = \frac{R_1.R_2}{R_1 + R_2 + R_3} \; \; \text{-------- equation 6}$

$R_c = \frac{R_2.R_3}{R_1 + R_2 + R_3} \; \; \text{-------- equation 7}$

The relation of delta - star transformation can be expressed as follows. The equivalent star resistance connected to a given terminal, is equal to the product of the two delta resistances connected to the same terminal divided by the sum of the delta connected resistances. If the delta connected system has same resistance $R$ at its three sides then equivalent star resistance $r$ will be,

$r = \frac{R.R}{R+R+R} = \frac{R}{3}$

Star To Delta Conversion

For star - delta transformation we just multiply equations (5), (6) and (6), (7) and (7), (5) that is by doing (5) x (6) + (6) x (7) + (7) x (5) we get,

$R_aR_b + R_bR_c + R_cR_a =$ $\frac{R_1.R_2^2.R_3 + R_1.R_2.R_3^2 + R_1^2.R_2.R_3}{(R_1 +R_2 + R_3)^2}$

$= \frac{R_1.R_2.R_3(R_1 + R_2 + R_3)}{(R_1 + R_2 + R_3)^2}$

$= \frac{R_1.R_2.R_3}{R_1 + R_2 + R_3} \; \; \text{-------- equation 8}$

Now dividing equation (8) by equations (5), (6) and equations (7) separately we get,

$R_1 = \frac{R_aR_b + R_bR_c + R_cR_a}{R_c}$

$R_2 = \frac{R_aR_b + R_bR_c + R_cR_a}{R_a}$

$R_3 = \frac{R_aR_b + R_bR_c + R_cR_a}{R_b}$

For the reverse transformation, the star-delta transformation, the equivalent delta resistance connected between any two terminals in the delta configuration would be three times the equivalent star resistance connected to those same terminals. Therefore:

$R = 3r$