Mesh And Nodal Analysis

Mesh Analysis

• Mesh analysis is based on Kirchhoff's Voltage Law (KVL) which states that the sum of the voltages around any closed loop in a circuit must be zero.

• In mesh analysis, the circuit is divided into meshes, which are the smallest possible loops in the circuit that do not enclose any other loops. For an n-node circuit with b branches, there will be n - 1 meshes.

• In each mesh, a loop equation is formed using KVL. This equation relates the voltages across elements in the mesh to the currents flowing through them.

• After obtaining the loop equations for each mesh, the equations are solved simultaneously to find the mesh currents.

• Mesh analysis is particularly useful for circuits with multiple interconnected loops.

Steps for Mesh Analysis:

1. Identify Meshes: Identify the independent loops in the circuit. Each mesh is a loop that does not enclose any other loops.

2. Assign Mesh Currents: Assign a current variable to each mesh (e.g., $I_1$,$I_2$,....,$I_n$). The direction of the current is usually assumed to be clockwise, but it can be arbitrary.

3. Apply KVL: Apply Kirchhoff's Voltage Law (KVL) around each mesh. Sum the voltage drops around the loop, setting the sum equal to zero.

4. Solve the Equations: Solve the resulting system of linear equations for the mesh currents.

Numerical

Ques: Find the current I (current through 10 ohm resistor) using Mesh Analysis.

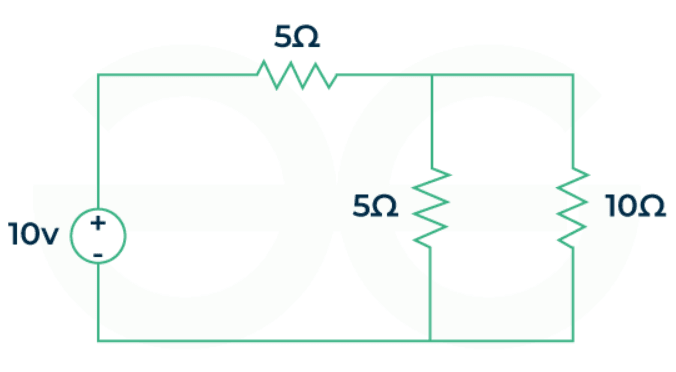
Sol:

We first analyze the circuit and as it is planar we move forward with the mesh analysis. Next, we observe that the network has two meshes and then assign current $I_1$ and $I_2$ to the meshes respectively.

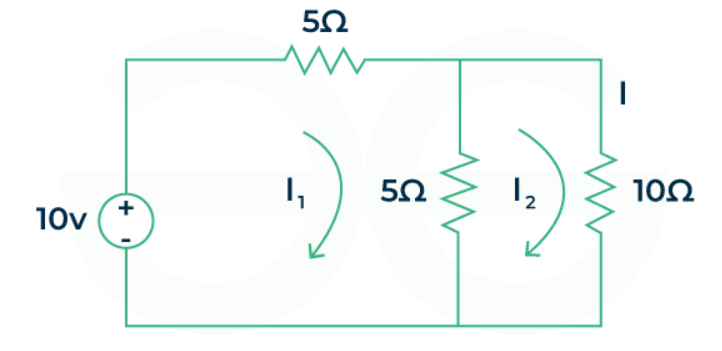
Developing the KVL equation for the Mesh-1,

$$10 - 5I_1 - 5(I_1 - I_2) = 0$$ $$⇒ 2I_1 - I_2 = 2 -(1)$$

Developing the KVL equation for the Mesh-2,

$$- 5(I_2 - I_1) - 10I_2 = 0$$ $$⇒ 3I_2 - I_1 = 0 -(2)$$

Solving equation (1) and (2) ,

$$⇒ 3I_2 = I_1 \quad \text{from (2)}$$

Putting values in (1)

$$⇒ 6I_2 - I_2 = 2$$ $$⇒ I_2 = \frac{2}{5} = 0.4A$$ $$⇒ ∵ I_2 = I$$ $$∴ I = 0.4A$$

Nodal Analysis

• Nodal analysis is based on Kirchhoff's Current Law (KCL) which states that the algebraic sum of currents entering and leaving a node in a circuit is zero.

• In nodal analysis, the circuit is analyzed by considering the voltages at each node (connection point) in the circuit.

• One node is chosen as the reference node (usually the ground or negative terminal of the power supply), and the voltages at all other nodes are defined relative to this reference node.

• KCL equations are written for each non-reference node, relating the currents flowing into and out of each node.

• After obtaining the KCL equations for each node, the equations are solved simultaneously to find the node voltages.

• Nodal analysis is particularly useful for circuits with many interconnected nodes.

Steps for Nodal Analysis

1. Identify Nodes: Identify all the nodes in the circuit. Choose one node as the reference node (ground).

2. Assign Node Voltages: Assign a voltage variable to each node (except the reference node).

3. Apply KCL: Apply Kirchhoff's Current Law (KCL) at each node (except the reference node). Sum the currents entering and leaving the node, setting the sum equal to zero.

4. Solve the Equations: Solve the resulting system of linear equations for the node voltages.

Numerical

Ques: Using nodal analysis find the value of K which will cause $V_y$ to be zero

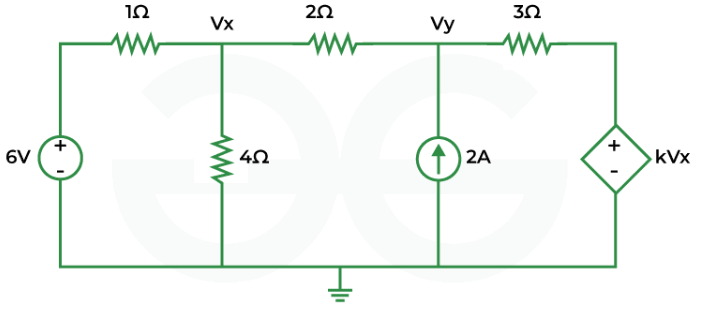
Sol:

Using KCL at node x,

$(V_x - 6) \times 1$ + $V_x \times 4$ + $(V_x - V_y) \times 2$ = 0

$V_y$ = 0

$4V_x - 24 + V_x + 2V_x$ = 0

$V_x$ = $24/7V - (1)$

KCL at node y,

$(V_y - V_x) \times 2 + (V_y -kV_x) \times 3$ = 2

Substituting value of Vy and Vx

∴​ $(-24/7) \times 2$ – $k \times (24/7) \times 3$ = 2

$-12 – 8k = 14$

$k = -3.25$