Electrodynamics

Electrodynamics is the branch of physics that studies the behavior and interactions of electric and magnetic fields. It deals with the forces exerted by these fields on charged particles and the subsequent motion of these particles.

Equation of Continuity

The continuity equation is an equation that describes the transport of some quantities like fluid or gas. It is also known as the transport equation. The continuity equation is very simple and powerful when it is applied to a conserved quantity. When it is applied to an extensive quantity it can be generalized. Physical phenomena are conserved using continuity equations like energy, mass, momentum, natural quantities, and electric charge.

The equation of continuity is a principle derived from the conservation of mass, which states that the mass flow rate of a fluid must remain constant from one cross-section of a pipe to another if the fluid is incompressible and there are no sources or sinks of mass within the flow.

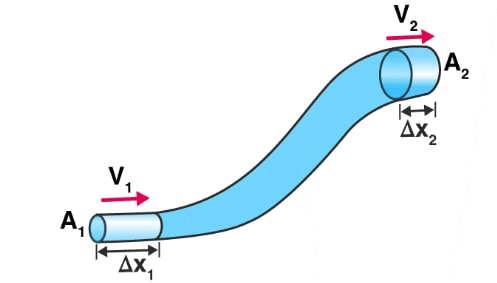
According to the continuity equation:

$$A_1 V_1 = A_2 V_2$$

Where,

• $A_1$ = cross-sectional area of region 1
• $V_1$ = flow velocity in region 1
• $A_2$ = cross-sectional area of region 2
• $V_2$ = flow velocity in region 2

Continuity equations are a local and stronger form of conservation laws. For example, a weak version of the law of conservation of energy states that energy can neither be created nor destroyed, which means that the total amount of energy in the universe is fixed. It means energy can neither be created nor destroyed nor can it teleport from one place to another—it can only move by continuous flow.

A continuity equation is nothing but a mathematical way to explain this kind of statement. The continuity equation consists of many other transport equations like the convection-diffusion equation, Navier–Stokes equations, and the Boltzmann transport equation.

Convection–Diffusion Equation: It is a combination of convection and diffusion equations. It describes the physical phenomena where particles, energy, and other physical quantities are transferred with the help of 'diffusion and convection' inside a physical system.

Boltzmann Transport Equation: The Boltzmann transport equation describes the behavior (statistical in nature) of the thermodynamic system, which is not in the state of rest or equilibrium.

Continuity Principle

The continuity principle refers to the principle of fluid mechanics. The principle of the continuity equation is a consequence of the law of conservation of mass. Through the continuity equation, the behavior of fluid is described when it is in motion. The second equation is based on Newton's law of motion (which describes the motion of an object and the force acting on its flow), and the third equation is based on the law of conservation of energy (which states that mass can neither be created nor destroyed).

Differential Form of the Continuity Equation

The differential form of the continuity equation states that the divergence of the current density $\mathbf{J}$ is equal to the negative rate of change of the volume charge density $\rho$. Mathematically, this is expressed as:

$\nabla \cdot \mathbf{J} = -\frac{\partial \rho}{\partial t}$

This equation conveys that:

• The divergence of the current density $\mathbf{J}$ (which represents the net outflow of charge per unit volume) is equal to the negative rate of change of the volume charge density $\rho$ (which represents the amount of charge per unit volume).
• If the current density $\mathbf{J}$ has a net outflow from a region (i.e., $\nabla \cdot \mathbf{J} > 0$ ), the charge density $\rho$ within that region decreases over time.
• Conversely, if the current density $\mathbf{J}$ has a net inflow into a region (i.e., $\nabla \cdot \mathbf{J} < 0$), the charge density $\rho$ within that region increases over time.

This relationship is fundamental in the study of electromagnetism, as it ensures the conservation of charge.

Integral Form of the Continuity Equation

The integral form of the continuity equation says that:

• When additional q flows inward through the surface of the region, the amount of q in a region increases.
• When q flows outward, the amount of q decreases.
• When new q is created inside a region, the amount of q increases.
• When q is destroyed, the amount of q decreases.

Apart from these two methods, there is no other way for the amount of q in a region to change.

In terms of mathematics, the integral form of the continuity equation expressing the rate of increase of q within a volume V is:

$$\frac{d}{dt} \int_V q \, dV + \oint_S \mathbf{J} \cdot \mathbf{dS} = \sum$$

Here,

• S denotes an imaginary closed surface that encloses a volume V,
• $\oint_S J . \mathbf{dS}$ is a surface integral over that closed surface S,
• q denotes the total amount of the quantity in volume V,
• $\mathbf{J}$ is the flux of q,
• $t$ denotes time,
• And $\sum$ is the net rate that q is being produced inside the volume V.

Displacement Current

Displacement current is the current that is produced by the rate of change of the electric displacement field. It differs from the normal current that is produced by the motion of the electric charge. Displacement current is the quantity explained in Maxwell’s Equation. It is measured in Ampere.

The concept of displacement current was introduced by James Clerk Maxwell to address a gap in Ampère's circuital law in the context of time-varying electric fields. It is essential for the consistency of Maxwell's equations and the understanding of electromagnetic waves.

Definition:

The displacement current $I_d$ is defined as:

$$I_d = \epsilon_0 \frac{d\Phi_E}{dt}$$

where:

• $\epsilon_0$ is the permittivity of free space.
• $\Phi_E$ is the electric flux through a surface $S$, defined as $\Phi_E = \int_S \mathbf{E} \cdot \mathbf{dS}$, where $\mathbf{E}$ is the electric field and $\mathbf{dS}$ is the differential area vector.

Significance

1. Consistency in Maxwell's Equations - The introduction of the displacement current term ensures the consistency of Maxwell's equations, particularly in scenarios involving time-varying electric fields.

2. Electromagnetic Waves - The displacement current is crucial for the propagation of electromagnetic waves. Without it, the changing electric field in a vacuum would not produce a magnetic field, and vice versa, thereby preventing the propagation of waves.

3. Charging and Discharging of Capacitors - The displacement current provides a mechanism to describe the changing electric fields between the plates of a capacitor, allowing for a continuous description of the current in the circuit.

Characteristics of Displacement Current

• In an electric circuit, there are two types of current that are conduction current and the other is Displacement current. Various characteristics of displacement current are mentioned below:

• Displacement current does not appear from the actual movement of the electric charge as in the case of the conduction current but is produced by time changing electric field.

• Displacement current is a vector quantity.

• Electromagnetic waves propagate with the help of displacement current