Introduction and Discovery of Superconductivity
Topic asked in Applied Physics 2023 (CBCS/NEP) question paper Section D - 8(a).
Superconductivity is a phenomenon where a material can conduct electric current with zero electrical resistance. This means that an electric current can flow indefinitely without any energy loss in a superconducting material. This effect occurs below a certain critical temperature , known as the superconducting transition temperature.
Discovery of Superconductivity
Superconductivity was first discovered by Dutch physicist Heike Kamerlingh Onnes in 1911. While studying the electrical properties of mercury at very low temperatures, Onnes observed a sudden drop in electrical resistance to zero when the mercury was cooled to 4.2 Kelvin (K). Generally good conductors like Au, Ag, Cu, Li, Na, K, etc. do not show superconductivity even at absolute zero.
-
Heike Kamerlingh Onnes (1911):
- Experiment: Onnes was investigating the behavior of materials at cryogenic temperatures using liquid helium.
- Observation: At 4.2 K, the resistance of mercury dropped abruptly to zero, a phenomenon Onnes described as "superconductivity."
-
Meissner-Ochsenfeld Effect (1933):
- Discovery: Walter Meissner and Robert Ochsenfeld discovered that superconductors expel magnetic fields, known as the Meissner effect.
-
BCS Theory (1957):
- Developers: John Bardeen, Leon Cooper, and Robert Schrieffer developed the first microscopic theory of superconductivity, known as BCS theory.
- Explanation: BCS theory explained superconductivity as a result of electron pairing (Cooper pairs) mediated by lattice vibrations (phonons).
Understanding Superconductivity
- Critical Temperature : The temperature below which a material becomes superconducting.
- Zero Electrical Resistance: Superconductors can carry an electric current indefinitely without any energy loss.
- Meissner Effect: Superconductors expel magnetic fields from their interior, maintaining zero magnetic flux inside.
- Type I and Type II Superconductors:
- Type I: Exhibit a complete Meissner effect and have a single critical magnetic field.
- Type II: Have two critical magnetic fields and allow partial penetration of magnetic fields in quantized vortices.
Meissner Effect
The Meissner effect is a fundamental property of superconductors that distinguishes them from perfect conductors. It describes the complete expulsion of magnetic fields from the interior of a superconducting material when it transitions into the superconducting state below its critical temperature This effect demonstrates that superconductivity is not merely the absence of electrical resistance but also involves a unique interaction with magnetic fields.
The Meissner effect describes the complete expulsion of magnetic fields from the interior of a superconducting material when it transitions below its critical temperature
Discovery of the Meissner Effect
The Meissner effect was discovered in 1933 by Walther Meissner and Robert Ochsenfeld. They observed that when a superconducting material was cooled below its critical temperature in the presence of a magnetic field, the magnetic field inside the material was expelled, resulting in a zero internal magnetic field.
Explanation of the Meissner Effect
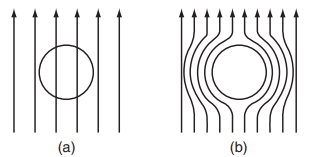
-
Magnetic Field Expulsion: When a material is placed in a magnetic field, the magnetic flux lines pass through it (as shown in Fig a). When the material transitions into the superconducting state, it actively expels magnetic fields from its interior, a phenomenon that is not observed in perfect conductors (as shown in Fig b). In perfect conductors, existing magnetic fields would be trapped inside the material, while in superconductors, these fields are expelled, leading to:
or
where,
- is the magnetic flux density,
- is the permeability of free space,
- is the magnetic field strength,
- is the magnetization of the material.
From this, we have:
The magnetic susceptibility is defined as:
In superconductors, since , the susceptibility is:
This means the material becomes an "ideal diamagnetic" in its superconducting state, exhibiting perfect diamagnetism.
If a superconductor is exposed to a strong enough magnetic field, it can lose its superconducting properties and revert to a normal state. This phenomenon is related to the material's critical magnetic field strength, beyond which superconductivity is destroyed (as shown in Fig a).
-
Surface Currents: The expulsion of the magnetic field is facilitated by the generation of surface currents in the superconductor. These currents create a magnetic field that opposes and cancels the external magnetic field within the material, ensuring that the magnetic field inside is zero.
-
London Equations: The behavior of the Meissner effect is described by the London equations, formulated by brothers Fritz and Heinz London in 1935. These equations provide a theoretical framework for understanding the electromagnetic properties of superconductors. The key London equation relevant to the Meissner effect is:
where is the superconducting current density, is the density of superconducting electrons, e is the electron charge, m is the electron mass, and is the magnetic field.
-
Penetration Depth: The magnetic field is not completely zero at the surface of the superconductor. Instead, it decays exponentially over a characteristic length called the penetration depth (). The London penetration depth is typically on the order of tens to hundreds of nanometers for most superconductors::
where is the magnetic field just outside the surface, and is the distance into the superconductor and is the penetration depth.
Significance and Applications
-
Fundamental Understanding: It provides a clear distinction between superconductors and perfect conductors, emphasizing that superconductivity is a quantum state with unique electromagnetic properties.
-
Applications in Technology:
-
Magnetic Levitation (Maglev): The expulsion of magnetic fields enables the phenomenon of magnetic levitation, used in maglev trains and other applications.
-
MRI Machines: Superconducting magnets, which leverage the Meissner effect, are essential in producing stable and strong magnetic fields for Magnetic Resonance Imaging (MRI).
-
Quantum Computing: Superconducting qubits used in quantum computers rely on the unique properties of superconductors, including the Meissner effect, to maintain quantum coherence.
-
The Meissner effect is a cornerstone in understanding superconductivity and has significant implications for various advanced technologies.
Types of Superconductors
Topic asked in Applied Physics 2023 (CBCS/NEP) question paper Section D - 8(b).
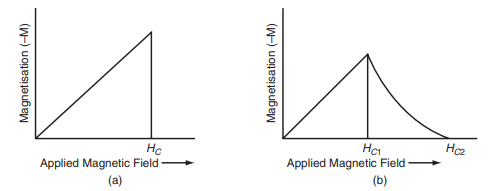
Superconductors are broadly classified into two types based on their behavior in the presence of magnetic fields: Type-I and Type-II superconductors.
Type-I (Soft) Superconductor
Type-I superconductors exhibit a complete Meissner effect. They expel all magnetic fields from their interior and become "ideal diamagnetic" materials when in the superconducting state. When subjected to an external magnetic field, the magnetization produced in the superconductor is in the opposite direction to the applied field, as shown in Fig. a. As the external magnetic field approaches the critical field , , the magnetization abruptly decreases, and the material transitions to a normal (non-superconducting) state. Above this critical magnetic field, the magnetic flux lines penetrate the material completely, and the superconductor loses its superconducting properties.
Characteristics of Type I Superconductors
-
Single Critical Magnetic Field : When the external magnetic field exceeds , the material transitions from the superconducting state to the normal state.
-
Complete Meissner Effect: In the superconducting state, Type I superconductors expel all magnetic fields, maintaining zero magnetic flux inside the material.
-
Superconducting Transition: The transition from the superconducting state to the normal state is sharp and occurs uniformly throughout the material when the critical magnetic field is reached.
-
Materials: Type I superconductors are typically pure elemental metals, such as:
- Lead (Pb)
- Mercury (Hg)
- Aluminum (Al)
- Tin (Sn)
Type-II (Hard) Superconductor
Type-II superconductors display a more complex behavior compared to Type-I. Instead of an abrupt transition, Type-II superconductors exhibit a gradual loss of magnetization. As depicted in Fig. b, when the external magnetic field is increased from zero, flux lines start to penetrate the material at the lower critical field .
In the range between and (the upper critical field), the material is in a "mixed state" or "vortex state," where magnetic flux lines penetrate the superconductor in discrete vortices while still maintaining zero electrical resistivity. When the external magnetic field exceeds , the superconductor transitions to a normal conductor, and the superconducting state is completely destroyed.
Characteristics of Type II Superconductors
-
Two Critical Magnetic Fields:
- Lower Critical Field : Below , the superconductor expels all magnetic fields.
- Upper Critical Field : Above , the superconductor transitions to the normal state.
-
Mixed State (Vortex State): Between and , Type-II superconductors exhibit a mixed state where magnetic flux lines penetrate the material in discrete vortices, but the material still maintains zero electrical resistivity.
-
Applications: Due to their higher critical magnetic fields and better performance in high magnetic field applications, Type II superconductors are widely used in technological applications such as:
- High-field magnets (e.g., MRI machines, particle accelerators)
- Power transmission lines
- Magnetic levitation systems (maglev trains)
-
Materials: Type II superconductors include various compounds and alloys, such as:
- Niobium-titanium (NbTi)
- Niobium-tin
- Yttrium barium copper oxide (YBCO)
- Bismuth strontium calcium copper oxide (BSCCO)
| Characteristic | Type-I Superconductors | Type-II Superconductors |
|---|---|---|
| Magnetic Field Behavior | Complete expulsion of magnetic fields; ideal diamagnetic behavior. | Partial expulsion; magnetic flux penetrates in vortices in the mixed state. |
| Critical Magnetic Fields | Single critical magnetic field at which superconductivity is lost. | Two critical magnetic fields: lower critical field and upper critical field . |
| Magnetization | Magnetization abruptly decreases and the material becomes normal when is exceeded. | Magnetization decreases gradually between and ; complete loss of superconductivity above . |
| Mixed State | No mixed state; material transitions directly from superconducting to normal state. | Exhibits a mixed state (vortex state) between and , where magnetic flux lines penetrate in vortices. |
| Applications | Used in low magnetic field applications and less common in modern technology. | Widely used in high-field applications, such as MRI machines, particle accelerators, and maglev trains. |
| Examples | Lead (Pb), Mercury (Hg), Aluminum (Al), Tin (Sn). | Niobium-titanium (NbTi), Niobium-tin (Nb3Sn), Yttrium barium copper oxide (YBCO), Bismuth strontium calcium copper oxide (BSCCO). |
Isotope Effect
The isotope effect is observed in superconductors where the critical temperature is affected by the isotopic mass of the constituent elements. This effect provides insights into the mechanisms underlying superconductivity, particularly in conventional superconductors explained by BCS theory.
Discovery and Historical Context
The isotope effect was first discovered in 1950 by Emanuel Maxwell and, independently, by C.A. Reynolds, B. Serin, W.H. Wright, and L.B. Nesbitt. They observed that the of mercury superconductors varied with different isotopes of mercury.
Theoretical Explanation
-
BCS Theory
- According to BCS theory, superconductivity arises from the formation of Cooper pairs bound by an attractive interaction mediated by lattice vibrations (phonons).
- The isotope effect supports the BCS theory, indicating that the electron-phonon interaction is crucial for Cooper pair formation. The phonon frequency is inversely proportional to the square root of the atomic mass M:
- This relationship, known as the isotope effect, is expressed as: where is the isotope effect exponent, typically around 0.5 for conventional superconductors.
-
Mathematical Formulation
- For a superconductor with isotopic substitution, the critical temperature changes according to: where and are the critical temperatures before and after the isotope substitution, and M and M' are the masses of the original and substituted isotopes.
Experimental Observations
-
Mercury: The first observations were made with mercury isotopes, showing variations as predicted by the isotope effect formula.
-
Other Elements: Subsequent experiments confirmed the isotope effect in other elemental superconductors like lead (Pb) and tin (Sn).
Significance and Implications
-
Support for BCS Theory: Provides strong evidence for the electron-phonon interaction as the driving force behind superconductivity in conventional superconductors.
-
Insights into Mechanisms: Helps understand the nature of the pairing mechanism and the role of lattice vibrations.
-
High-Temperature Superconductors: In HTS, the isotope effect is weak or absent, suggesting different mechanisms for superconductivity.
The isotope effect is a cornerstone in understanding the fundamental principles of superconductivity and the role of lattice vibrations in the formation of the superconducting state.
BCS Theory (Qualitative)
Topic asked in Applied Physics 2023 (CBCS/NEP) question paper Section D - 8(a).
The quantum theory of superconductivity is primarily based on the 1957 paper by John Bardeen, Leon Cooper, and Robert Schrieffer, commonly known as BCS theory. This theory applies broadly, from atoms in their condensed phase to both Type-I and Type-II metallic superconductors. It posits that electron interactions mediated through lattice vibrations (phonons) are central to superconductivity.
Basis of BCS Theory
BCS theory is grounded in two key experimental observations:
-
Isotope Effect:
- The isotope effect demonstrated that the critical temperature of superconductors varies with the atomic mass of the constituent elements. Specifically, decreases as the atomic mass increases, approaching zero as becomes very large. This indicates that lattice vibrations play a crucial role in superconductivity, as the transition temperature is dependent on the finite mass of the ions in the lattice.
-
Variation of Specific Heat:
- A discontinuous jump in specific heat at indicates the presence of an energy gap in the electron energy spectrum in the superconducting state. This energy gap is essential for understanding the superconducting transition.
Theoretical Explanation
-
Electron-Phonon Interaction:
- In the BCS framework, an electron approaching a positive ion core experiences an attractive Coulomb interaction, causing the ion core and the surrounding lattice to distort. This distortion is greater when the mass of the positive ion is smaller. A second electron interacting with this distorted lattice experiences a lowered energy. Thus, the two electrons interact via the lattice distortion, mediated by phonons, resulting in an attractive interaction between them.
-
Cooper Pairs:
- The fundamental postulate of BCS theory is that superconductivity occurs when an attractive interaction between two electrons, mediated by phonons, dominates over the usual repulsive interaction. The two electrons involved in this attractive interaction form a Cooper pair. The energy of these pairs in a bound state is lower than that of free electrons. This binding energy, which is the energy required to break the pair, is maximum when the electrons have opposite momenta and spins. At absolute zero temperature (0 K), the pairing is complete, while it is completely broken at the critical temperature .
-
BCS Wavefunction:
-
The BCS wavefunction describes a state composed of these Cooper pairs. According to BCS theory, this wavefunction accounts for the familiar superconductivity observed in metals and the associated energy gap. Key aspects of the BCS wavefunction include:
-
Energy Gap: The interaction between electrons leads to a ground state that is separated from excited states by an energy gap. This gap influences thermal and many electromagnetic properties of superconductors.
-
Flux Quantization: The magnetic flux through a superconducting ring is quantized, with the effective unit of charge being rather than . This quantization reflects the coherent nature of the superconducting state.
-
-
High Temprature Superconductors
High-temperature superconductors (HTS) are materials that exhibit superconductivity at temperatures significantly higher than those of conventional superconductors. The discovery of HTS has led to extensive research due to their potential applications in various technological fields.
Discovery and Background
-
Initial Discoveries:
Superconductivity was first discovered in mercury by Heike Kamerlingh Onnes in 1911 at a temperature of 4.2 K. For many years, superconductors were limited to temperatures below 30 K. This changed in 1986 when Johannes Georg Bednorz and Karl Alexander Müller discovered superconductivity in a lanthanum barium copper oxide (LaBaCuO) ceramic material at approximately 35 K. This groundbreaking discovery earned them the Nobel Prize in Physics in 1987.
-
Yttrium Barium Copper Oxide (YBCO):
Shortly after the discovery by Bednorz and Müller, other researchers found that replacing lanthanum with yttrium in the ceramic compound increased the transition temperature to 92 K. This compound, yttrium barium copper oxide (YBCO), became the most well-known high-temperature superconductor because its critical temperature is above the boiling point of liquid nitrogen (77 K).
Characteristics of High-Temperature Superconductors
-
Cuprates:
Most high-temperature superconductors discovered so far are copper oxide (cuprate) materials. They typically have a layered perovskite structure with copper-oxygen planes where superconductivity primarily occurs.
-
Transition Temperatures:
High-temperature superconductors have transition temperatures (Tc) that are much higher than those of conventional superconductors, often exceeding 100 K. For example, (Hg-1223) has a of 133 K under normal pressure, which can be increased to around 164 K under high pressure.
-
Unconventional Mechanisms:
Unlike conventional superconductors, where the electron-phonon interaction is the primary mechanism, the exact mechanism for superconductivity in high-temperature superconductors is still not completely understood. Theories suggest that electron-electron interactions within the copper-oxygen planes play a crucial role.
Applications of High-Temperature Superconductors
-
Magnetic Levitation (Maglev):
HTS materials are used in magnetic levitation (maglev) trains. These trains use powerful superconducting magnets to lift and propel the train above the tracks, reducing friction and allowing for high speeds.
-
Medical Imaging:
High-temperature superconductors are employed in magnetic resonance imaging (MRI) machines. The strong magnetic fields required for MRI can be generated more efficiently with HTS materials.
-
Power Cables and Transformers:
HTS materials are used to manufacture power cables and transformers, which can transmit electricity with minimal loss due to their zero resistance.
-
Scientific Research:
HTS materials are utilized in various scientific instruments, including particle accelerators and other research facilities requiring strong magnetic fields and efficient current transmission.
Application Of Superconductivity
Superconductivity is a fascinating phenomenon characterized by the complete absence of electrical resistance in certain materials when they are cooled below a critical temperature. This property has several practical applications, including:
-
Magnetic Resonance Imaging (MRI):
MRI machines use superconducting magnets to create strong, stable magnetic fields required for imaging internal body structures. The superconductors allow for high field strengths with low energy consumption.
-
Maglev Trains:
Superconducting magnets are employed in magnetic levitation (maglev) trains. These trains float above the tracks, reducing friction and allowing for extremely high speeds and smooth rides.
-
Particle Accelerators:
Superconducting magnets are used in particle accelerators, such as the Large Hadron Collider (LHC), to steer and focus particle beams at high energies, enabling groundbreaking research in particle physics.
-
Electric Power Cables:
Superconducting materials can be used in power cables to transmit electricity with minimal energy losses. This application is particularly useful in reducing power dissipation in long-distance transmission lines.
-
Magnetic Energy Storage:
Superconducting Magnetic Energy Storage (SMES) systems store and release large amounts of energy with high efficiency. They are useful for stabilizing power grids and providing backup power.
-
Quantum Computing:
Superconductors are essential in the development of quantum computers. Superconducting qubits, which are the basic units of quantum information, can perform complex computations far more efficiently than classical bits.
-
Medical and Scientific Instruments:
Superconducting materials are used in various scientific instruments, including ultra-sensitive magnetometers (SQUIDs) for measuring tiny magnetic fields and in NMR spectrometers for analyzing molecular structures.
-
Fusion Reactors:
In the quest for practical nuclear fusion, superconducting magnets are used to confine plasma within fusion reactors. Projects like ITER rely on superconductivity to achieve the necessary magnetic fields for sustaining fusion reactions.
-
Electric Motors and Generators:
Superconducting materials can improve the efficiency and power density of electric motors and generators, making them more effective for applications in transportation and renewable energy systems.
-
Magnetic Levitation Devices:
Superconductivity is applied in various levitation devices beyond trains, such as for contactless bearings and flywheels in mechanical systems, enhancing performance and reducing wear and tear.